Условие симметричного
размещения сателлитов можно получить,
учитывая, что число зубьев центральных зубчатых колёс планетарной передачи
должно быть распределено поровну на каждый из сателлитов:
za = (zb + za)/nw,
или (zb + za)/nw = целое число ,
где nw – число сателлитов.
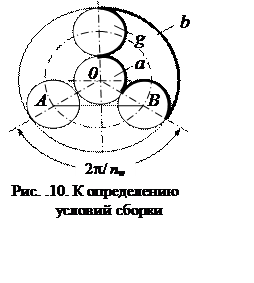
Условие соседства сателлитов следует из недопустимости соприкосновения зубьев соседних сателлитов:
АВ = 2АО sin p/nw, где АО = ra + rg и АВ > 2 (rg + m).
Следовательно, (ra +rg) sin p/nw > 2 (rg + m). Умножив на 2 и разделив на m, получим
(za + zg) sin p/nw > zg + 2.
Очевидно, что при таком количестве условий возможный набор передаточных отношений и чисел зубьев колёс ограничен. При проектировании планетарных передач приходится руководствоваться специальными таблицами возможных вариантов передаточных отношений и чисел зубьев.
.3. ПЕРЕДАТОЧНЫЕ ОТНОШЕНИЯ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ
Вначале рассмотрим планетарную передачу 2k с одним неподвижным звеном.
Определим передаточное отношение при передаче движения от солнечного колеса а к водило h методом плана скоростей. Скорость точки А контакта начальных окружностей солнечного колеса и сателлита равна vа = = wаra (рис. .11, а). Точка С контакта начальных окружностей сателлита g и эпицикла b является мгновенным центром вращения сателлита. Следовательно, скорость оси Ow сателлита vog = 0,5 vа = 0,5wаra. С другой стороны, скорость vog = wh (ra + rg), где wh – угловая скорость водила. Из равенства 0,5wаra = wh (ra + rg) получим передаточное отношение ibah планетарной передачи при передаче движения от колеса а к водило h при неподвижном колесе b:
ibah = wа /wh = 2(ra + rg)/ ra = 2[ra + (rb – ra)/2]/ ra = (ra + rb)/ra = 1 + zb /za.
|
|
ibha = wh/wа = 1/ibah = ra /(ra +rb) = za/( zb
+ za)
= .
ihab = wа /
wb = – zb /za.
Заметим, что отношение (– zb /za) равно передаточному отношению ihab планетарной передачи от колеса а к колесу b при неподвижном водило h
Знак «– » означает, что направления вращения колеса а и b противоположны (рис. 11, б).
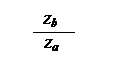Таким образом, между передаточными отношениями имеет
место зависимость
ibah = 1 + = 1 – ihab = 1/ibha
Согласно методу Виллиса для определения передаточного отношения ibah планетарной передачи от солнечного колеса а к водило h при непод-вижном эпицикле b достаточно определить передаточное отношение ihab простой передачи (при неподвижном водило) с учётом направления вращения колёс и использовать соотношение ibah = 1 – ihab.
Общность данного метода можно обосновать следующим образом. Пусть все колёса и водило подвижны. Тогда передаточное отношениеiHAB при движении от колеса A к колесу B равно отношению угловых скоростей этих колёс, взятых относительно водила H, т.е.
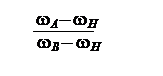iHAB =
.
(Так как векторы угловых скоростей всех колёс параллельны, то разность угловых скоростей определяется как разность их модулей).
Аналогично запишем передаточное отношение от колеса A к водило H при вращении колеса B с угловой скоростью wB:
 |
.
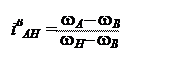Выполним преобразование разности (1 – ihab ):
 |
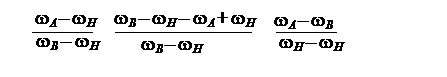1 – iHAB = 1 – = = = iBAH.
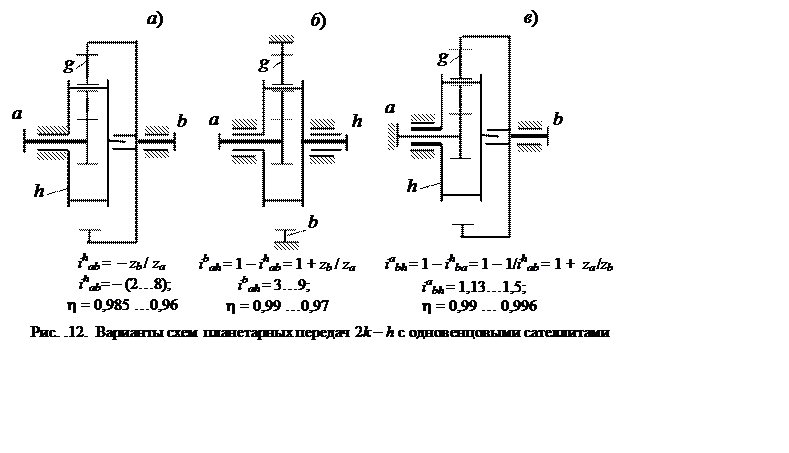
На рис. .12 показаны наиболее распространённые планетарные передачи 2k и указаны их рациональные передаточные отношения.
Последовательное соединение двух планетарных передач ibah (рис. .9, б) позволяет получить передаточные отношения от 12 до 50 при КПД от 0,98 до 0,94. А последовательное соединение двух планетарных передач ihab (рис. .12, а) и ibah (рис. .12, б) обеспечивает передаточное отношение от 10 до 50 при КПД от 0,975 до 0,93. Вторая комбинации предпочтительнее, так как водило быстроходной ступени ihab неподвижно и поэтому опоры сателлитов разгружены от действия центробежных сил
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.