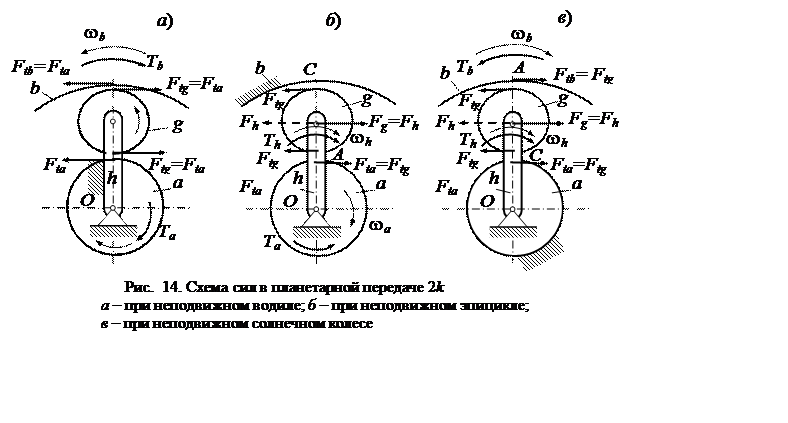
При неподвижном солнечном колесе (рис. .14, в) силы определяются аналогично предыдущему случаю. Момент на колесе bравен Тb = –Ftgrb = = – 0,5Fhrb = – 0,5 Тhrb/(rа+ rg).
Отношение Тb/Тh = – 0,5rb /(rа+ rg) = –1/(1 + zа /z b) = – 1/ iabh.
При определении межосевого расстояния по критерию контактной прочности зубьев необходимо знать момент Т1, диаметр шестерни d1 и передаточное отношение u. Для передач на рис. 14 в каждом из зацеплений центрального колеса с сателлитом выделяют меньший (шестерню z1) и больший (колесо z2) элемент этой пары. Принимают u = z2 / z1 и определяют Т1 с учётом числа сателлитов и неравномерности распределения нагрузки между сателлитами:
Т1 = Т2 Кс / (nwu),
где Т2 – момент на колесе z2;
Кс – коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами, зависит от точности изготовления и числа сателлитов; при nw = 3 и самоустанавливающемся солнечном колесе принимают Кс = 1,1 … 1,2.
Коэффициент ширины венца yba = bb /(ra +rg), где bb – ширина венца эпицикла b, принимают
yba = 0,4 при твёрдости поверхности зубьев Н £ 350 НВ,
yba = 0,315 при твёрдости поверхности зубьев 350 НВ £ Н £ 50 НRC,
yba = 0,25 при твёрдости поверхности зубьев Н > 50 НRC.
Ширина венца сателлита bg » bb + 2т, а солнечного колеса – bа = 1,1 bg.
При оценке усталостной прочности зубьев при изгибе следует учитывать, что зуб сателлита нагружается дважды (в зацеплении с колесом а и колесом б), причём направление сил в этих зацеплениях противоположны. Поэтому, определяя допускаемые напряжения, вводят коэффициент YA, учитывающий двухстороннее нагружение зубьев:
YA = 0,65 для стали после улучшения;
YA = 0,75 после закалки ТВЧ или цементации;
YA = 0,9 после азотирования.
Назначение остальных коэффициентов и выбор допускаемых напряжений аналогичен обычным зубчатым передачам.
Выбор подшипников опор сателлитов определяется также необходимостью ослабить влияние перекосов на распределение нагрузки по длине зубьев. Преимущественно используются сферические шарикоподшипники, а при значительных радиальных нагрузках – роликовые сферические подшипники. С целью уменьшения габаритов применяют также игольчатые подшипники и подшипники скольжения.
Значение КПД планетарных передач рассчитывается по специальным формулам. В зависимости от схемы передачи, ведущего колеса и других факторов может быть как выше, так и ниже обычных зубчатых передач с равным передаточным отношением.
ВОЛНОВЫЕ ПРЕДАЧИ
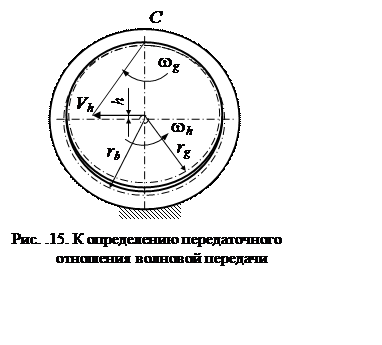
Преобразуем схему на рис. .8 так, чтобы число зубьев сателлита zgоказалось несколько меньше числа зубьев колеса zb, или rb » rg (рис. .15).
Скорость оси сателлита Vh = whhравна линейной скорости при вращении сателлита относительно мгновенного центра вращения в т. С. Соответственно, угловая скорость сателлита равна wg = – wh h/rg = – wh(rb – rg) и передаточное отношение
ibhg = – wh/wg = – zg/(zb– zg).
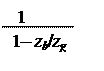Значение ibhg можно определить, используя метод Виллиса:
ibhg = 1/ ibgh = 1/(1– ihgb) = ;
ibhg = – zg/(zb– zg).
Аналогично получим передаточное отношение при не вращающемся сателлите ighb =1/ igbh = 1/(1– ihbg) = 1/(1–zg/zb) = zb/(zb– zg). При rb » rg можно получить передаточное отношение сотни крат.
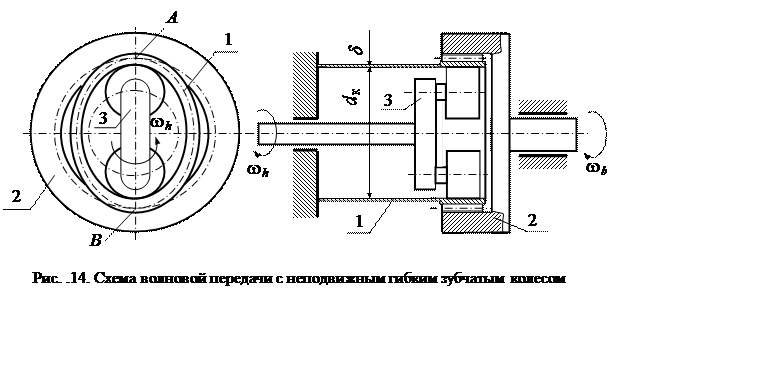
Так как сателлит, не вращаясь, должен «обегать» все зубья внешнего колеса, он изготавливается в виде тонкостенного гибкого цилиндра с зубьями на утолщённом конце (рис. .14). Деформация гибкого колеса g (1) в радиальном направлении при вращении водила обеспечивает контакт поочерёдно зубьев гибкого колеса g со всеми зубьями жёсткого внешнего колеса b(2). Водило в такой конструкции принято называть деформатором или генератором волн (3). Каждая точка гибкого колеса при вращении генератора волн совершает волнообразное движение. Поэтому передачи такого вида названы волновыми.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.