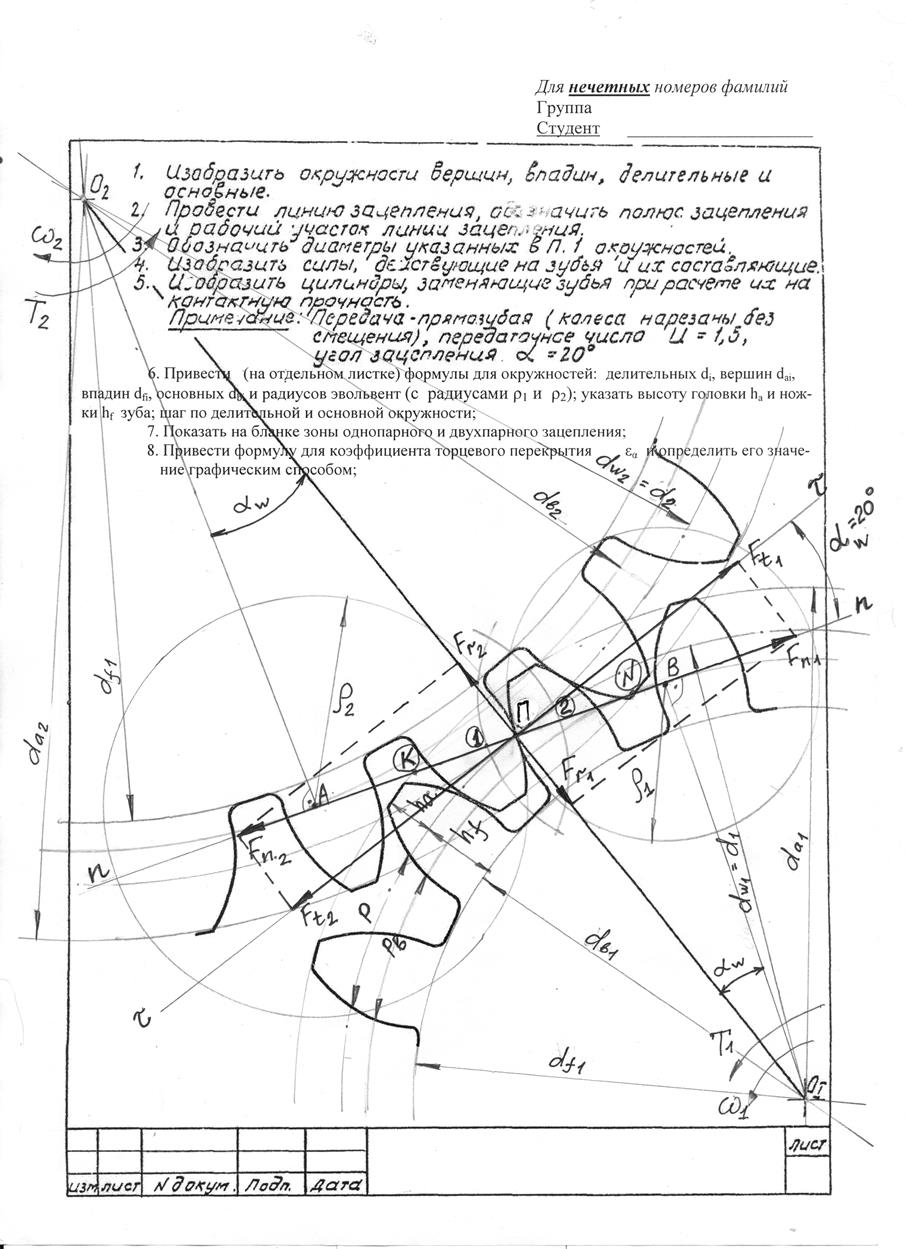
Геометрические параметры прямозубой цилиндрической передачи (Последовательность заполнения бланка зубчатого зацепления)

ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ПРЯМОЗУБОЙ

ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ

Последовательность заполнения бланка зубчатого зацепления

1. Перпендикулярно линии межосевого расстояния О₁О₂, через точку касания двух эвольвентных контуров зубьев провести общую касательную τ – τ;

2. Перпендикулярно обеим эвольвентам в точке их касания на линии  О₁О₂, под углом α_w = 20⁰ (угол зацепления), провести линию n – n  – общую нормаль (линию зацепления);

3. Точка пересечения линии межосевого расстояния О₁О₂ общей нормалью (одновременно точка касания эвольвентных профилей) – является полюсом зацепления П;

                         ИЗ ОСНОВНОЙ ТЕОРЕМЫ ЗАЦЕПЛЕНИЯ:

… для обеспечения постоянного передаточного отношения зубчатых колес профили их зубьев должны очерчиваться кривыми, у которых общая нормаль (n – n), проведенная через точку касания профилей, делит расстояние между центрами на отрезки, обратно пропорциональные угловым скоростям …

3. Из точек  т.О₁ и т.О₂ восстановить перпендикуляры на общую нормаль (n – n) с точками пересечения т.А и т.В;

4. Из центров колес  О₁ и О₂ очертить и обозначить диаметры окружностей колес:

а) через т.П (полюс) – начальные окружности, совпадающие с делительными: d_wi = d_i, (в случае когда зубья колес нарезаны без смещения инструмента), где  i = 1,2;

б) через вершины зубьев – окружности вершин: d_ai = d_i + 2m;

в) через впадины – окружности впадин: d_fi = d_i – 2,5m;

г) радиусами О₁В и О₂В очертить диаметры основных окружностей: d_bi;

Определение окружностей:

-  Начальные окружности  d_wi в процессе зацепления перекатываются друг по другу без скольжения. При изменении межосевого расстояния  меняются и диаметры начальных окружностей. У пары зубчатых колес может быть множество начальных окружностей. У отдельно взятого колеса начальной окружности не существует.

                                             ;

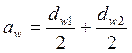-  Делительная окружность – окружность на которой шаг р и угол зацепления α_w соответственно равны шагу и углу профиля инструментальной рейки. Делительная окружность является физической окружностью и принадлежит отдельно взятому колесу. Делительные окружности совпадают с начальными (d_wi = d_i,), если колеса нарезаны без смещения, а также :       ;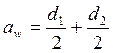

Длина делительной окружности составляет: πd_i = pz_i; откуда 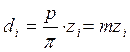; где m – модуль зацепления – один из главных параметров зубчатого зацепления; соответствует ГОСТ; модуль можно трактовать как часть диаметра делительной окружности, приходящейся на один зуб: m = d_i/z_i;

р – окружной шаг: расстояние между одноименными сторонами соседних зубьев, взятое по дуге делительной окружности р = s_t + e_t; где s_t – толщина зуба; e_t – ширина впадины; Сопряженные колеса должны иметь одинаковый окружной шаг;

-  Основная окружность (эволюта): окружность, по которой без скольжения перекатывается без скольжения производящая прямая (в данном случае n – n), точки которой описывают эвольвенты: d_bi = d_wicos α_w =  d_icos α_w;

Основной шаг p_b – измеряется по основной окружности: представляет расстояние по нормали между одноименными сторонами соседних зубьев

5. Расстояние между точками пересечения (т.N и т.K) общей нормали n – n (линии зацепления) с окружностями вершин зубьев отрезок NК является длиной активной линии зацепления:      q_α = NK;

6. Обозначить направление вращения колес:– угловая скорость ω₁ и момент Т₁ ведущей шестерни (с центром О₁) совпадают по направлению; для ведомого колеса (с центром О₂) направление момента полезного сопротивления Т₂ противоположно направлению угловой скорости ω₂, направленной навстречу ω₁;

7. Обозначить окружной р и основной р_b шаги колес;

8. Обозначить высоту головки и ножки зуба соответственно: h_a = m;  h_f = 1,25m;

9. Радиусами ρ₁=ВП и ρ₂=АП соответственно обозначить диаметры цилиндров, которыми заменяются эвольвенты профилей зубьев при расчете по контактным напряжениям: ρ_i= d_i ∙sinα_w;

10. Определить графическим путем (измеряя соответствующие отрезки посредством линейки) коэффициент торцевого перекрытия: ;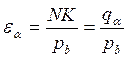

11. Обозначить на длине активной линией зацепления q_α зоны однопарного и двухпарного зацепления. Для этого из точек т.N и т.К  радиусом, равным шагу по основной окружности  р_b, сделать засечки. При этом отрезки К1и 2N – соответствуют двухпарному зацеплению, отрезок KN – однопарному зацеплению;

12. Обозначить векторы сил, действующих в зацеплении прямозубой передачи:

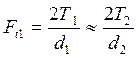-  - окружные составляющие  нормального усилия; при этом направление окружного усилия  F_t2 на ведомом колесе совпадает с направлением угловой скорости ω₂; направление окружного усилия  F_t1 на ведущего колеса противоположно  направлению угловой скорости ω₁;

-  - радиальные составляющие нормального усилия, направлены к центру соответствующих колес;

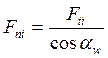-  - нормальные  усилия зацепления, направлены вдоль общей нормали (линии зацепления);