Статистическая проверка непараметрических гипотез

Курс лекций по дисциплине «ТВиМС»

Лекция №7                    (лекция №16 в общем потоке)

План:

·  Предисловие;

·  Постановка задачи проверки непараметрических гипотез;

·  Критерий «согласия» Пирсона (c²);

·  Критерий «согласия» А.Н. Колмогорова;

·  Послесловие.

Предисловие

На прошлой лекции рассмотрели основные понятия и идею проверки статистических гипотез и рассмотрели технологию проверки 4-х типов параметрических гипотез (относительно значения МО СВ, имеющей нормальное распределение с известным и неизвестным СКО, а также о равенстве МО двух СВ, имеющих нормальные законы распределения). На сегодняшней лекции займёмся проверкой непараметрических гипотез.

Постановка задачи проверки непараметрических гипотез

Следует напомнить, что статистическая гипотеза называется непараметрической, если в ней сформулировано предложение относительно вида функции распределения исследуемой СВ, т.е. H_o: F_x(x)=F^*(x).

Напомню также, что СВ полностью с вероятностной точки зрения характеризуются законами распределения. Если известен закон распределения СВ, то можно определить вероятности любых событий, связанных с данной СВ, определить точные значения числовых характеристик и т.п. К сожалению, часто на практике нельзя однозначно определить закон распределения исследуемой величины. Поэтому поступают следующим образом. Сначала на основании предметной постановки задачи и / или визуального анализа статистического закона распределения выдвигают предположение (гипотезу) о виде закона распределения, затем статистическими методами проверяют согласование данной гипотезы с экспериментальными данными.

Проверка гипотезы о предполагаемом распределении производится с помощью непараметрических статистических критериев значимости (вспомогательных СВ, которые имеют заранее известное распределение при условии верности гипотезы H_o).

Как обычно (для проверки параметрических), если выборочное значение статистического критерия значимости будет принадлежать области маловероятных критических значений (ÎОКЗ), то гипотеза H_o: F_x(x)=F^*(x) должна быть отклонена, как не согласующаяся с экспериментальными данными. Если же ÎОДЗ, то гипотеза H_o согласуется с экспериментальными данными, следовательно, оснований для её отклонений нет.

Следует отметить, что, как правило, альтернативной гипотезой является сложная гипотеза H_a: F_x(x)¹F^*(x), поэтому распределение статистического критерия в случае верности H_a однозначно не известно, следовательно, при исследовании гипотезы не контролируется вероятность совершения ошибки 2-го рода, т.е. принятия ложной гипотезы. Поэтому вывода о принятии гипотезы вовсе не делают.

Непараметрические критерии значимости условно делят на две группы. Это критерии «согласия» с помощью которых проверяются гипотезы относительно общего вида функции распределения (Пирсона, Колмогорова); и критерии «однородности», с помощью которых проверяются гипотезы о равенстве функций распределения двух СВ (или что тоже самое – о принадлежности двух выборок одной генеральной совокупности) (Вилкоксона).

Критерий «согласия» Пирсона (c²)

Критерий  «согласия» Пирсона (c²) позволяет проводить проверку согласия эмпирического и гипотетического (предполагаемого) законов распределения. Для этого

1.1. Строится статистический закон распределения x (для ДСВ – сгруппированный; для НСВ – интервальный).

1.2. На основании предметной постановки задачи или визуального анализа статистического закона распределения выдвигается гипотеза о виде функции распределения СВ x. Т.е. H_o: F_x(x)=F^*(x); H_a: F_x(x)¹F^*(x).

1.3. Оцениваются числовые характеристики СВ x и параметры гипотетической функции распределения F^*(x).

2. Для проверки гипотезы о виде функции распределения СВ x используется статистический критерий значимости

,                                                        (*)

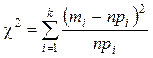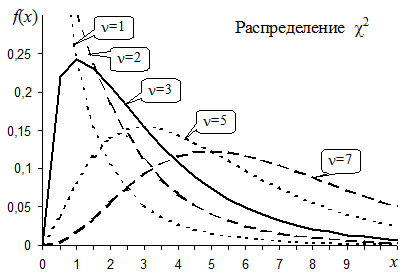
который (в случае верности H_o) независимо от вида гипотетического распределения F^*(x) имеет распределение c² с n=k–r–1 степенями свободы. Здесь m_i – количество значений СВ x, попавших в i-ю группу (интервал); k – количество групп (интервалов) статистического закона распределения; p_i – вероятность попадания значений СВ x в i-ю группу (интервал) при условии F_x(x)=F^*(x); n – объём выборки значений СВ x; r – количество параметров, определяющих функцию F^*(x).

3. Попадание значений СВ x в i-ю группу (интервал) есть испытания Бернулли. Следовательно, величина m_i (число попаданий в n испытаниях) имеет биномиальный закон распределения с параметрами n и p_i. Следовательно, M[m_i]=np_i.

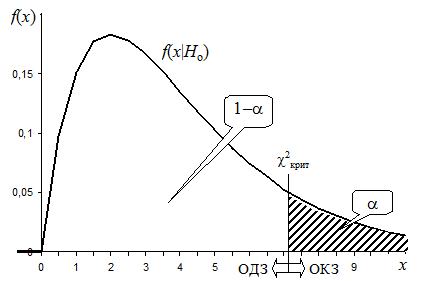
Т.о. в формуле (*) вычисляется отклонение фактической частоты попадания значений СВ x в i-ю группу (интервал) m_i от среднего значения np_i , ожидаемого при условии верности гипотезы H_o: F_x(x)=F^*(x). Если гипотеза H_o верна, то данные отклонения незначительны, и критерий значимости c² принимает малые значения. Если же H_o не верна, то отклонения фактических и ожидаемых частот будут значительны, а c²®¥. Таким образом, ОКЗ статистического критерия c² (см. рисунок) является правосторонней.

Для заданного уровня значимости a определяется величина ОКЗ из условия . Значение , – есть квантиль распределения c² с n=k–r–1 степенями свободы уровня a (определяется по таблицам).

4. Рассчитывается выборочное значение статистического критерия значимости .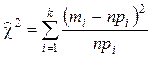

5. Если H_o: F_x(x)=F^*(x) верна, то  и значит . Если же , т.е. происходит практически невозможное событие, то с большой вероятностью (1–a) можно утверждать, что H_o не верна.

Т.о. если , то гипотеза H_o считается согласующейся с результатами опытов и оснований для отклонения гипотезы нет. Если , то гипотеза H_o не согласуется с экспериментальными данными, следовательно она отклоняется, и с вероятностью (1–a) можно утверждать, что верна H_a . При отклонении гипотезы можно, однако совершить ошибку 1-го рода, но вероятность такой ошибки равна a»0.

Критерий «согласия» Колмогорова А.Н.