Статистическая проверка непараметрических гипотез, страница 2

Критерий «согласия» Колмогорова применяется для проверки гипотез о виде функции распределения только непрерывных СВ, когда параметры гипотетического распределения точно известны. В качестве статистического критерия значимости используется величина l, равная максимальному отклонению эмпирической и предполагаемой (гипотетической) функции распределения случайной величины, т.е.

,                                                 (**)

где , F^*(x) – значения эмпирической и гипотетической функции распределения, соответственно; n – объём выборки. Т.о. критерий «согласия» Колмогорова сравнивает отклонения функций (эмпирической и гипотетической) распределения СВ.

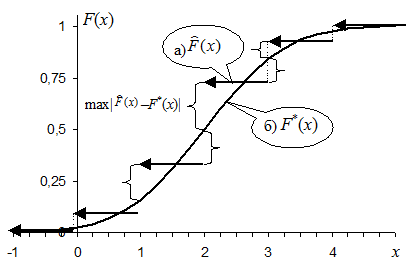
Например, если  СВ x имеет вид, представленный на графике «а», и при этом предполагается показательное распределение СВ x, т.е. F^*(x) имеет вид, представленный на графике «б», то отклонения выбираются следующим образом.

Колмогоров А.Н. доказал, что при n®¥, в случае справедливость гипотезы H_o: F_x(x)=F^*(x), статистический критерий l имеет функцию распределения вида: 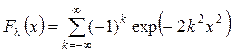, которая не зависит от гипотетического распределения F^*(x).

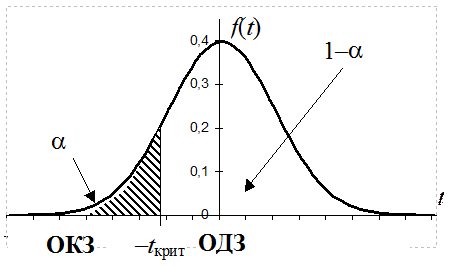
Если наблюдаемое значение <l_крит , то гипотеза H_o согласуется с результатами опытов и оснований для отклонения гипотезы нет. Если >l_крит , то гипотеза H_o не согласуется с экспериментальными данными; она отклоняется, и с вероятностью (1–a) можно утверждать, что верна H_a .

Задача. Время выполнения некоторого технологического процесса (ТП) имеет нормальный закон со средним значением 20 мин. Для сокращения времени выполнения данного ТП был проведён ряд мероприятий (автоматизация, изменение структуры ТП и т.п.). Значимо ли повлияли проведённые мероприятия на время выполнения ТП, если по результатам 30 испытаний среднее время выполнения ТП составило 18,9 мин, а среднеквадратическое отклонение – 3,3 мин? Построить доверительный интервал для МО времени выполнения ТП после модернизации.

Решение. Пусть x – время выполнения ТП. x~N(M[x],s[x]), причём M[x], s[x] – ? Однако ,  .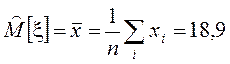

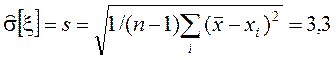Найдём доверительный интервал для M[x]:

.

Для данной гипотезы Ha  ОКЗ критерия t будет двухсторонней. tкрит=ta/2, n–1=t0,025, 29=2,045 . Поскольку , то гипотеза Ho: M[x]=20 согласуется с опытом. Т.е. проведённые меры значимо не сократили время выполнения ТП.

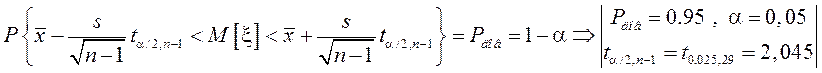
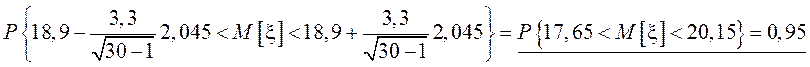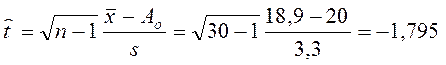Проверим гипотезу H_o: M[x]=20; H_a: M[x]¹20.  Т.к. x~N(M[x],s[x]) и s[x] – ?, то будем использовать критерий , где A_o – гипотетическое значение M[x].

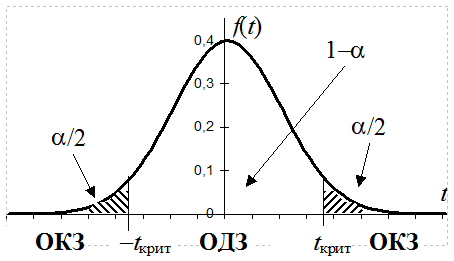
Пусть P{M[x]>20}=0, тогда  H_o: M[x]=20; H_a: M[x]<20.

Для данной гипотезы Ha  ОКЗ критерия t будет односторонней. tкрит=ta, n–1=t0,05, 29=1,699 . Т.к. , то Ho: M[x]=20 не согласуется с опытом, с вероятностью 1–a=0,95 можно утверждать, что верна гипотеза Ha: M[x]<20 (среднее время выполнения ТП после проведённых мероприятий значимо уменьшилось).

Критерий «согласия» Пирсона (c²)

1.1. Строится статистический закон распределения x.

1.2. Выдвигается гипотеза H_o: F_x(x)=F^*(x) и H_a: F_x(x)¹F^*(x).