Лабораторная работа №4
ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ СИСТЕМЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Цель работы: ознакомится с основными понятиями регрессионного и корреляционного анализа, изучить методику исследования зависимости между двумя случайными величинами.
Задание: построить эмпирическое уравнение регрессии вида ![]() и оценить тесноту зависимости между
изучаемыми переменными.
и оценить тесноту зависимости между
изучаемыми переменными.
Порядок выполнения работы.
Характер расположения точек на корреляционном поле позволяет сделать предположение о гиперболической регрессионной зависимости вида:
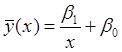
решая систему: ![]()
![]()
получим: ![]() =0,199493
=0,199493
![]() =19,8039
=19,8039
|
x |
1/(xx) |
1/x |
y |
(1/(x))y |
ß/x+ß |
(y(x) - y) |
( y - y ) |
|
1 |
1 |
1 |
20 |
20 |
20,00339 |
196,095 |
196 |
|
2 |
0,25 |
0,5 |
10 |
5 |
10,10144 |
16,82183 |
16 |
|
3 |
0,111111 |
0,333333 |
7 |
2,333333 |
6,800793 |
0,641269 |
1 |
|
4 |
0,0625 |
0,25 |
5 |
1,25 |
5,150468 |
0,721705 |
1 |
|
5 |
0,04 |
0,2 |
4 |
0,8 |
4,160273 |
3,384595 |
4 |
|
6 |
0,027778 |
0,166667 |
4 |
0,666667 |
3,500143 |
6,249285 |
4 |
|
7 |
0,020408 |
0,142857 |
3 |
0,428571 |
3,028622 |
8,82909 |
9 |
|
8 |
0,015625 |
0,125 |
3 |
0,375 |
2,674981 |
11,05575 |
9 |
|
9 |
0,012346 |
0,111111 |
2 |
0,222222 |
2,399926 |
12,96053 |
16 |
|
10 |
0,01 |
0,1 |
2 |
0,2 |
2,179883 |
14,59329 |
16 |
|
cумма |
1,549768 |
2,928968 |
60 |
31,27579 |
271,3524 |
272 |
|
R2 |
F |
S2 регр. |
S2 ост. |
F |
|
0,997619 |
3351,961 |
7,863188 |
1,15E-05 |
3355,588 |
|
0,010291 |
||||
|
0,039683 |
||||
|
0,022641 |
||||
|
0,025687 |
||||
|
0,249857 |
||||
|
0,000819 |
||||
|
0,105638 |
||||
|
0,159941 |
||||
|
0,032358 |
||||
|
0,646927 |
Уравнение регрессии примет вид: у(х)=19,8039*(х)-1+0,199493
Изображаем на диаграмме рассеивания линию регрессии: значения ординат берем из столбца ß /x+ß =у
Оценим качество зависимости м/у величиной Х и У, полученным уравнением регрессии с помощью коэффициента детерминации:
R2=S(y(x) - y)2/S( y - y ); R2=0,997619
Проверим значимость полученного значения R2:
F=0,997619*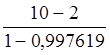 =3351,961
=3351,961
Критическое значение статистики Фишера для степеней свободы (1) и (8) и уровня значимости 0,05 составляет F0.05;1;8=5.318. Поскольку расчетные значения Фишера больше критического(3355,61>5,318), то вычисленный коэффициент детерминации значимо отличается от 0, поэтому выбранное уравнение регрессионной зависимости между X и Y
может быть использовано для описания изучаемого явления.
Проверим адекватность уравнения регрессии выборочным данным:
F= (S2 регр./n1)/( S2 ост./n2)
F=3355,588
Т.к. 3355,588 >4,737(F0,05;2;7=4,737),то проверяемую гипотезу об отсутствии между переменными Y и X зависимости гиперболического вида следует отклонить. Построенная регрессионная модель считается адекватной экспериментальным данным и может быть использована для описания изучаемого явления.
Вывод: на основании выборочных данных построили гиперболическое уравнение регрессии у(х)= 19,8039*(х)-1+0,199493. Установлено, что данное уравнение является адекватным выборочным значениям. Значение коэффициента детерминации составило 0,997619.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.