Расчет коэффициентов вариации по группировочному признаку на основании исходных и сгруппированных данных. Анализ показателей бухгалтерского баланса путем расчета статистических показателей структуры и динамики, страница 8

Раздел 3. Выборочный метод в статистических исследованиях

Задание 1

Провести 50% механическую выборку из совокупности данных Вашего варианта, приведенных в таблице 2, по результативному признаку, указанному в таблице 3. Начало отбора начинать с номера предприятия, совпадающего с номером Вашего варианта. С вероятностью 0,95 рассчитать по выборочной совокупности границы изменения средней величины и сравнить со средней, рассчитанной по всей исследуемой совокупности. Сформулировать вывод.

Решение

   Механическая выборка предполагает, что  отбор  единиц из генеральной совокупности производится через равные промежутки, т.е. через определенное число единиц.  По условию требуется провести 50%-ную выборку, следовательно, в выборочную совокупность должна попасть каждая вторая единица из генеральной совокупности. 

     Номер варианта - 5, поэтому отбор будет начинаться с 5-ого предприятия, и в выборку попадут предприятия со следующими номерами:5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39

    Таким образом, в выборочную совокупность попадут 18 предприятий.

  Данные о выборочной совокупности занесены в таблицу 16.

В этой же таблице проведем вспомогательные расчеты, необходимые для дальнейших вычислений.

Таблица 16

    Данные о выборочной совокупности

Для расчета границ изменения средней характеристики генеральной совокупности по материалам выборки использованы следующие формулы:

 - средняя генеральной совокупности;

 - средняя выборочной совокупности;

D _м.в.  - предельная ошибка малой выборки;

t - коэффициент доверия;

m _м.в.   -  средняя ошибка малой выборки;

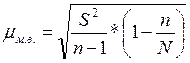
S² - дисперсия исследуемого показателя;

n - объем выборочной совокупности;

N - объем генеральной совокупности;

n/N - доля выборочной совокупности в объеме генеральной

(или процент отбора , выраженный в коэффициенте)

Средний объем чистой прибыли в выборочной совокупности равен:  

         =Sy_i/n=195423/18=10856,833 (тыс.руб.)

Дисперсия результативного признака равна:

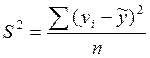         =3 618 690 214,500/18=201 038 345,250 (тыс.руб.)

t=t_{(1-a=1-0.05=0.95, k=n-1=16-1=15)}=2,132, т.к. вероятность определения границ средней - 0.95 (по условию)

Рассчитаем среднюю ошибку:

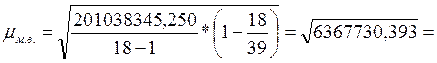2523,436 (тыс. руб.)

Рассчитаем предельную ошибку и определим границы изменения средней :

                    D_м.в.=t*m_м.в.=2,132*2523,436=5379,966

    Границы средней генеральной совокупности:

       10856,833-5379,966<<10856,833+5379,966

                                       или

                       5476,867<<16236,799