Экономика и менеджмент \ Статистика

Расчет коэффициентов вариации по группировочному признаку на основании исходных и сгруппированных данных. Анализ показателей бухгалтерского баланса путем расчета статистических показателей структуры и динамики, страница 2

  =970770/30=32359,000 (тыс. руб.) – средний объем запасов предприятия в выборочной совокупности

   Медиана (Мe) - это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньше, чем медиана, а другая - большие.

  В интервальном вариационном ряду порядок нахождения медианы следующий. Для ранжированного ряда определяются накопленные частоты, по данным о накопленных частотах находится медианный интервал. Медиана делит численность ряда пополам, следовательно, она находится в том интервале, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности. Для анализируемого ряда медиана расположена в интервале 22028,2 -37524,40, так как для этого интервала сумма накопленных частот, равная 22, больше половины всей суммы частот (30/2=15), а накопленная частота в непосредственно предшествующем интервале (12) меньше половины всей суммы частот.

     Расчет значения медианы осуществляется по следующей формуле:

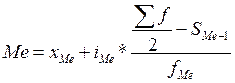
xMe - нижняя граница медианного интервала

iMe - величина медианного интервала

Sf/2 - полусумма частот ряда

SMe-1 - сумма накопленных частот, предшествующих медианному интервалу

fMe - частота медианного интервала

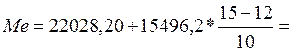 26677,060 (тыс. руб.)

Модой (Мо) называется чаще всего встречающееся в совокупности значение признака.   Для определения моды в интервальном ряду с равными интервалами  сначала определяют модальный интервал, которому соответствует максимальная частота. Для анализируемых данных наибольшую частоту (12) имеет интервал 6532-22028,20.

Значение моды внутри интервала определяется по формуле:

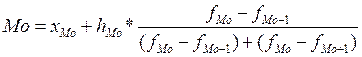
xМо - нижняя граница модального интервала

hМо - длина модального интервала

fМо - частота модального интервала

fМо-1 - частота интервала, предшествующего модальному

fМо+1 - частота интервала, следующего за модальным

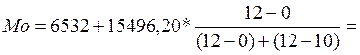 19814,457 (тыс. руб.)

 Наиболее точным показателем асимметрии является моментный коэффициент асимметрии (As):

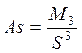
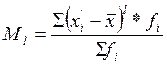 - центральный  момент l-ого порядка

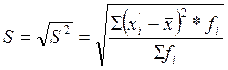 - среднее квадратическое отклонение

Расчет центральных моментов осуществлен в таблице 5.


Таблица 5

Группы предприятий по объему запасов

 fi

х'i

(xi- )2*fi

(xi-)3*fi

(xi-)4*fi

6532-22028,20

12

14280,10

3 922 159 502,520

-70 908 329 430 108,800

1 281 944 596 934 000 000,000

22028,20-37524,40

10

29776,30

66 703 392,900

-172 274 852 842,829

444 934 262 437 175,000

37524,40-53020,60

3

45272,50

500 275 446,750

6 460 306 981 606,120

83 425 174 206 970 700,000

53020,60-68516,8

1

60768,70

807 111 054,090

22 929 782 913 380,700

651 428 253 634 271 000,000

68516,80-84013,00

4

76264,90

7 710 912 219,240

338 554 540 806 730,000

14 864 541 813 206 200 000,000

S

30

13 007 161 615,500

296 864 026 418 765,000

16 881 784 772 243 900 000,000

S/Sfi

433 572 053,850

9 895 467 547 292,160

562 726 159 074 796 000,000

          S==20822,393

S3=20822,3933=9 028 007 736 599,150

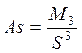=9 895 467 547 292,160/9 028 007 736 599,150=1,096

Оценка степени существенности показателя асимметрии дается с помощью средней квадратической ошибки,(SAs):

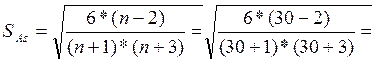0,405

   =1,096/0,405=2,705

s=2,705<3, следовательно, асимметрия в рассматриваемом ряду является несущественной, и ее наличие объясняется влиянием случайных обстоятельств. Положительная величина показателя асимметрии (As=1,096>0) указывает на наличие правосторонней асимметрии. Наличие правосторонней асимметрии так же подтверждается соотношением Мо<Ме<:

Мо=19814,457<Ме=26677,060<=32359,000

Скачать файл