Расчет коэффициентов вариации по группировочному признаку на основании исходных и сгруппированных данных. Анализ показателей бухгалтерского баланса путем расчета статистических показателей структуры и динамики, страница 3

Применяются так же структурные показатели ( коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения (т.е. основной массы единиц, и не зависящие от крайних значений признака). Рассчитаем структурный коэффициент асимметрии Пирсона (As_П) по формуле:

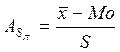
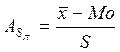= (32359,000-19814,457)/20822,393=0,602

As_П=0,602>0, что подтверждает вывод о правосторонней асимметрии, сделанные выше.

Эксцесс определяется только для симметричных и умеренно асимметричных распределений.

Эксцесс (Ex) оценивается с помощью показателя, рассчитываемого  по формуле:

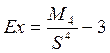
Расчет центрального момента 4-ого порядка осуществлен в таблице 5

S⁴=20822,393⁴=187 984 725 879 707 000,000

Ex=562 726 159 074 796 000,000/187 984 725 879 707 000,000-3=-0,007

Ex=-0.007<0 Þ распределение является более плосковершинным по сравнению с нормальным распределением

Чтобы оценить существенность эксцесса рассчитывают статистику:

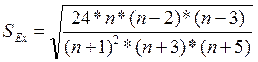
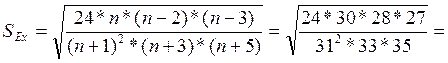0,700

=0,007/0,700=0,01

Отношение =0,01<3, следовательно, отклонение от нормального распределения является несущественным.

 Таким образом,  анализируемое распределение характеризуется незначительной правосторонней асимметрией, и  является более плосковершинным по сравнению с нормальным распределением.

Задание 2

    Для выявления зависимости между экономическими показателями деятельности предприятий провести аналитическую группировку. Рассчитать коэффициенты вариации по группировочному признаку на основании исходных и сгруппированных данных. Объяснить расхождения в значениях полученных коэффициентов.

Номера предприятий 5-34.

Y - результативный признак (прибыль от продажи, тыс. руб.)

Х - группировочный признак (запасы, тыс. руб.)

Таблица 6

      Исходные данные

Величина интервала группировки (d) определяется по формуле: 

d=(X_max-X_min)/k,

где k - количество групп

Х_max - максимальное значение группировочного признака

Х_min - минимальное значение группировочного признака

X_min=6532             X_max=84013

              d=(84013-6532)/5=15496,20

Далее определим границы для каждой группы.

Определение границ групп осуществлено таблице 7.

Таблица 7

Значения границ интервалов для проведения группировки

Группировку проведем в таблице 8