Итоговый тест по дисциплине "Теория автоматического управления" (Тест состоит из 217 вопросов, разделенных на четыре группы), страница 9

в) верны все выше названные ответы;

(Ф1 – ЗСр)

103)  Для какого процесса вводится понятие устойчивость?

а) установившегося ;

б) переходного;

в) переходного и установившегося одновременно;

(Ф1 – ЗСр)

104)  Какое уравнение считается характеристическим?

а) дифференциальный оператор при выходной величине приравненный к нулю;

б) дифференциальный оператор находящийся в знаменателе передаточной функции приравненный к нулю;

в) верны все выше названные ответы;

(Ф1 – ЗСр)

105)  Условие устойчивости линейной системы

а) для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения были правыми;

б) для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть;

в) для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения были левыми;

(Ф1 – ЗСр)

106)  Расположение каких корней на комплексной плоскости является признаком устойчивости САУ?

а) P₁, P₂, P₃;

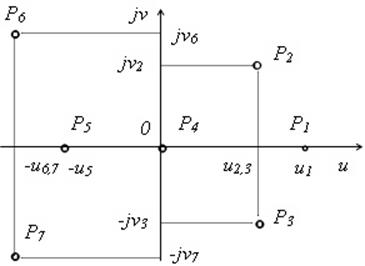б) P₄, P₅, P₆, P₇;

в) P₁, P₂, P₃, P₄, P₅, P₆, P₇;

г) P₅, P₆, P₇;

(Ф1 – ЗСр)

107)  Расположение каких корней на комплексной плоскости является признаком неустойчивости САУ?

а) P₁, P₂, P₃;

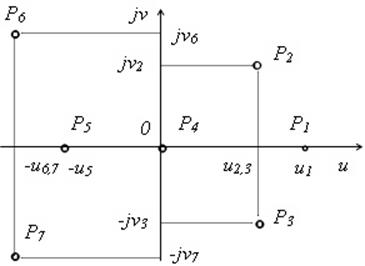б) P₄, P₅, P₆, P₇;

в) P₁, P₂, P₃, P₄, P₅, P₆, P₇;

г) P₅, P₆, P₇;

(Ф1 – ЗСр)

108)  Расположение каких корней на комплексной плоскости является признаком того, что САУ находится на границе устойчивости?

а) P₁, P₂, P₃;

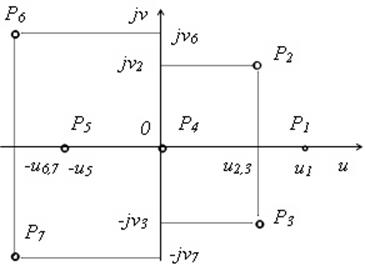б) P₄, P₅, P₆, P₇;

в) P₁, P₂, P₃, P₄, P₅, P₆, P₇;

г) P₅, P₆, P₇;

д) P₄

(Ф1 – ЗСр)

109)  Чьи критерии устойчивости относятся к алгебраическим?

а) Михайлова, Найквиста;

б) Михайлова, Рауса;

в) Гурвица, Рауса;

г) Гурвица, Найквиста

(Ф1 – ЗЛ)

110)  Характеристическое уравнение системы имеет вид:

р² + 7р + 12 = 0. Определить, будет ли САУ в замкнутом состоянии устойчива?

а) признаком устойчивости системы второго порядка является наличие левых корней p₁=-3, p₂=-4 ;

б) признаком устойчивости системы второго порядка является положительность коэффициентов характеристического уравнения, следовательно, система устойчива;

в) верны все выше перечисленные ответы;

(Ф1 – ЗСр)

111)  Для уравнений какого порядка положительность коэффициентов является необходимым и достаточным признаком устойчивости?

а) для уравнений первого порядка;

б) для уравнений первого и второго порядка;

в) для уравнений первого, второго и третьего порядка;

(Ф1 – ЗСр)

112)  Критерии устойчивости Рауса и Гурвица позволяет

а) по корням характеристического уравнения сделать суждение об устойчивости системы;

б) по коэффициентам характеристического уравнения без вычисления его корней сделать суждение об устойчивости системы;

в) по виду их частотных характеристик судить об устойчивости системы;

(Ф1 – ЗСр)

113)  Сущность критерия устойчивости Гурвица

а) САУ устойчива, если АФЧХ при изменении частоты от 0 до ¥, начинаясь при w=0 на вещественной положительной полуоси обходила против часовой стрелки число квадрантов координатной плоскости равное номеру характеристического уравнения;

б) САУ устойчива, если коэффициенты первого столбца таблицы имеют один и тот же знак, т.е. при первом коэффициенте больше нуля были больше нуля;

в) САУ устойчива, если все определители имеют знаки, одинаковые со знаками первого коэффициента характеристического уравнения, т.е. при a₀ > 0 были больше нуля;

(Ф1 – ЗСр)

114)  Для САУ имеющей характеристическое уравнение четвертого порядка признаком устойчивости по критерию Гурвица является выполнения условия

а) a₀ > 0;  a₁ > 0;  a₂ > 0; a₃ > 0;    а₄>0; a₁a₂ – a₀a₃ > 0;

б) a₀ > 0;  a₁ > 0; a₂ > 0;  a₃ > 0;  а₄>0; а₃(а₁а₂ – а₀а₃) – а₄ > 0;

в) a₀ > 0;  a₁ > 0; a₂ > 0;  a₃ > 0;  а₄>0;

(Ф1 – ЗСр)

115)  Для САУ имеющей характеристическое уравнение третьего порядка признаком устойчивости по критерию Гурвица является выполнения условия