Итоговый тест по дисциплине "Теория автоматического управления" (Тест состоит из 217 вопросов, разделенных на четыре группы), страница 10

а) a₀ > 0;  a₁ > 0;  a₂ > 0; a₃ > 0;    а₄>0; a₁a₂ – a₀a₃ > 0;

б)a₀ > 0;  a₁ > 0; a₂ > 0;  a₃ > 0;  а₄>0; а₃(а₁а₂ – а₀а₃) – а₄ > 0;

в) a₀ > 0;  a₁ > 0; a₂ > 0;  a₃ > 0;  а₄>0;

(Ф1 – ЗСр)

116)  Характеристическое уравнение имеет вид: 5р³ + 3р² +6р + 1 = 0, Используя критерий устойчивости Гурвица выберите правильный ответ.

а) все коэффициенты уравнения больше нуля, определитель второго порядка D₂=13> 0 следовательно, система устойчива

б) все коэффициенты уравнения больше нуля, определитель второго порядка D₂= -3< 0, следовательно, система неустойчива

в) все коэффициенты уравнения больше нуля, определитель второго порядка D₂= -13< 0, следовательно, система неустойчива

(Ф1 – ЗСр)

117)  Используя критерий устойчивости Гурвица, определить устойчивость САУ, если её характеристическое уравнение имеет вид: 3р³ + 5р² + 4р + 6 = 0,

где: а₀ = 3;     а₁ = 5;    а₂ = 4;     а₃ = 6.

а) Условие устойчивости:a₀ = 3 > 0;      a₁ = 5 > 0;      a₂ = 4 > 0;    a₃ = 6 > 0;D₂ > 0

Выразим определители Гурвица:

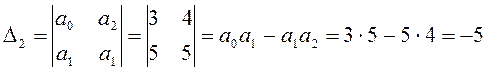
Условие D₂> 0 не выполняется, следовательно, система неустойчива.

б) Условие устойчивости:a₀ = 3 > 0;      a₁ = 5 > 0;      a₂ = 4 > 0;    a₃ = 6 > 0;D₂ > 0

Выразим определители Гурвица:

.

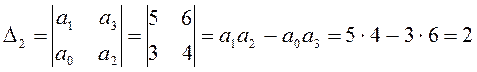Условие D₂> 0 выполняется, следовательно, система устойчива.

в) Условие устойчивости:  a₀ = 3 > 0;      a₁ = 5 > 0;      a₂ = 4 > 0;    a₃ = 6 > 0

Условие  выполняется, следовательно, система устойчива.

(Ф1 – ЗСр)

118)  Используя критерий устойчивости Гурвица, определить устойчивость САУ, если её характеристическое уравнение имеет вид: 5р³ + 2р² + 2р + 1 = 0,

где: а₀ = 5;     а₁ = 2;    а₂ = 2;     а₃ = 1

а) Условие устойчивости:a₀ = 5 > 0;  a₁ = 2 > 0;  a₂ = 2 > 0;  a₃ = 1 > 0;D₂ > 0

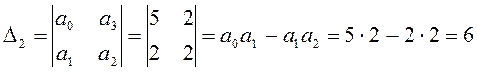
Условие D₂> 0 выполняется, следовательно, система устойчива.

б) Условие устойчивости::a₀ = 5 > 0;      a₁ = 2 > 0;      a₂ = 2 > 0;    a₃ = 1 > 0;D₂ > 0

.

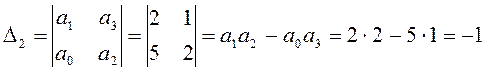Условие D₂> 0 не выполняется, следовательно, система неустойчива.

в) Условие устойчивости:  a₀ = 5 > 0;      a₁ = 2 > 0;      a₂ = 2 > 0;    a₃ = 1 > 0;D₂ > 0

Условие D₂> 0 выполняется, следовательно, система устойчива

(Ф1 – ЗСр)

119)  Используя критерий устойчивости Гурвица, определить устойчивость САУ, если её характеристическое уравнение имеет вид:

2р³ + 5р² +3р + 2 = 0,

а) все коэффициенты уравнения больше нуля, определитель второго порядка D₂=11> 0 следовательно, система устойчива

б) все коэффициенты уравнения больше нуля, определитель второго порядка D₂=4> 0, следовательно, система устойчива

в) все коэффициенты уравнения больше нуля, определитель второго порядка D₂= -2< 0, следовательно, система неустойчива

(Ф1 – ЗСр)

120)  Характеристическое уравнение имеет вид: р³ + 3р² +4р + 1 = 0, Используя критерий устойчивости Гурвица выберите правильный ответ.

а) все коэффициенты уравнения больше нуля, определитель второго порядка D₂=10> 0 следовательно, система устойчива

б) все коэффициенты уравнения больше нуля, определитель второго порядка D₂= -10< 0, следовательно, система неустойчива

в) все коэффициенты уравнения больше нуля, определитель второго порядка D₂= 9> 0, следовательно, система устойчива

(Ф1 – ЗСр)

121)  Критерий устойчивости Найквиста

а) если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф устойчивой разомкнутой системы «охватывал» точку (-1; i0)

б) если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф устойчивой разомкнутой системы «не охватывал» точку (-1; i0)

в) если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф устойчивой разомкнутой системы «не охватывал» точку (-1; i0)

(Ф1 – ЗСр)