88) Логарифмической амлитудно-частотной характеристикой (ЛАЧХ) L(w) называют
а) график зависимости модуля частотной характеристики от частоты, представленной в логарифмическом масштабе;
б) график зависимости аргумента частотной характеристики от частоты, представленной в логарифмическом масштабе;
в) график зависимости фазовой частотной функции от логарифма частоты;
(Ф1 – ЗСр)
89) Для построения логарифмической амплитудно-частотной характеристики переходят к выражению:
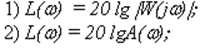
а) 1
б) 2
(Ф1 – ЗСр)
90) Декада соответствует
а) удвоенному значению частоты;
б) удесятеренному значению частоты;
(Ф1 – ЗЛ)
91) Изменение усилия на 20 Дб, соответствует изменению отношения двух амплитуд
а) в 10 раз;
б) в 20 раз;
в) в 2 раза;
г) в 100 раз;
(Ф1 – ЗСр)
92) Логарифмической фазовой частотной характеристикой (ЛФЧХ) называют
а) график зависимости модуля частотной характеристики от частоты, представленной в логарифмическом масштабе;
б) график зависимости аргумента частотной характеристики от частоты, представленной в логарифмическом масштабе;
в) график зависимости фазовой частотной функции от логарифма частоты;
(Ф1 – ЗСр)
93) В теории автоматического управления выделяют следующие типовые динамические звенья
а) стабилизации, программные, следящие;
б) замкнутое, разомкнутое, по возмущению, комбинированное;
в) безинерционное (пропорциональное), апериодическое (инерционное), дифференцирующее, интегрирующее, колебательное; запаздывающее;
(Ф1 – ЗСр)
94) Безинерционным называют
а) звено, в котором при подаче на вход ступенчатого сигнала выходная величина апериодически (по экспоненте) стремится к новому установившемуся значению;
б) звено, у которого выходная величина в каждый момент времени пропорциональна входной величине;
в) звено, в котором выходная величина пропорциональна производной во времени от входной величины;
г) звено, у которого при ступенчатом изменении входной величины выходная величина стремится к новому установившемуся значению, совершая при этом колебания;
(Ф1 – ЗСр)
95) Интегрирующим звеном называют
а) звено, в котором при подаче на вход ступенчатого сигнала выходная величина апериодически (по экспоненте) стремится к новому установившемуся значению;
б) звено, в котором выходная величина пропорциональна интегралу во времени от входной величины;
в) звено, в котором выходная величина пропорциональна производной во времени от входной величины;
г) звено, у которого при ступенчатом изменении входной величины выходная величина стремится к новому установившемуся значению, совершая при этом колебания;
(Ф1 – ЗСр)
96) Колебательным звеном называют
а) звено, в котором при подаче на вход ступенчатого сигнала выходная величина апериодически (по экспоненте) стремится к новому установившемуся значению;
б) звено, в котором выходная величина пропорциональна интегралу во времени от входной величины;
в) звено, в котором выходная величина пропорциональна производной во времени от входной величины;
г) звено, у которого при ступенчатом изменении входной величины выходная величина стремится к новому установившемуся значению, совершая при этом колебания;
(Ф1 – ЗСр)
97) Уравнение колебательного звена
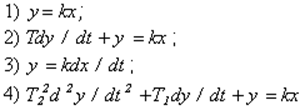
а) 1
б) 2
в) 3
г) 4
(Ф1 – ЗСр)
98) Уравнение безынерционного (пропорционального) звена
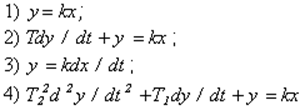
а) 1
б) 2
в) 3
г) 4
(Ф1 – ЗСр)
99) Уравнение дифференцирующего звена
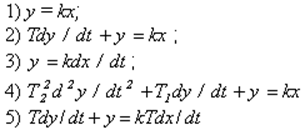
а) 1
б) 2
в) 3
г) 4
д) 5
(Ф1 – ЗСр)
100) Уравнение апериодического звена
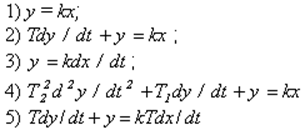
а) 1
б) 2
в) 3
г) 4
д) 5
(Ф1 – ЗСр)
101) Назовите характеристики динамических звеньев
а) переходная характеристика, АФЧХ, АЧХ, ФЧХ, ЛАЧХ;
б) временные, частотные, логарифмические;
в) верны все выше перечисленные ответы;
(Ф1 – ЗСр)
Раздел 3
Ф1
102) Под устойчивостью системы понимается
а) свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия;
б) малое изменение исходных данных должно приводить к малому изменению результатов;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.