Итоговый тест по дисциплине "Теория автоматического управления" (Тест состоит из 217 вопросов, разделенных на четыре группы), страница 18

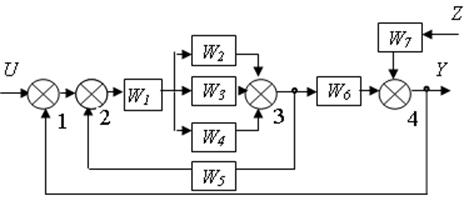
1 Преобразуем параллельно соединенные звенья W₁; W₂; W₃ к одному звену с передаточной функцией: W₈ = W₂ + W₃ + W₄;

2 Преобразуем последовательно соединенные звенья W₁, W₈ к одному звену
 с передаточной функцией: W₉ = W₁ (W₂ + W₃ + W₄);

3 Преобразуем обратную связь к звену с передаточной функцией: W₁₀ = W₁ (W₂ + W₃ + W₄)/ (1–W₁W₅(W₂ +W₃ + W₄));

4 Преобразуем последовательно соединенные звенья W₁₀ и W₆ к одному звену с передаточной функцией: W₁₁ = W₁W₆(W₂ +W₃+W₄)/(1–W₁W₅(W₂ +W₃ + W₄));

5. Перенесем сумматор 4 влево через звено W₁₁, добавляем к сумматору передаточную функцию звена в степени минус единица; Сумматор 4 переносим через сумматор 1 в начало схемы;

 (Ф3 – ЗТ)

3)  Используя правила структурных преобразований упростить структурную схему до одного звена с одной обратной связью, указать этапы преобразований

1 Преобразуем последовательно соединенные звенья W₁и W₃ к одному звену с передаточной функцией: W₄ = W₁ *  W₃;

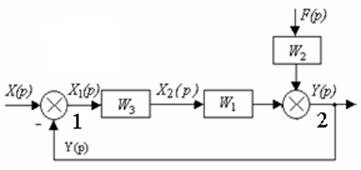2 Сумматор 3 переносим через звено с передаточной функцией W₄(p) добавляя к сумматору передаточную функцию W₄(p)в степени минус единица W₅(p) = W₂(p)/(W₁(p)×W₃(p);

3 Переносим сумматор 2 через сумматор 1 в начало схемы;

 (Ф3 – ЗТ)

4)  Используя правила структурных преобразований упростить структурную схему до одного звена с одной обратной связью, указать этапы преобразований

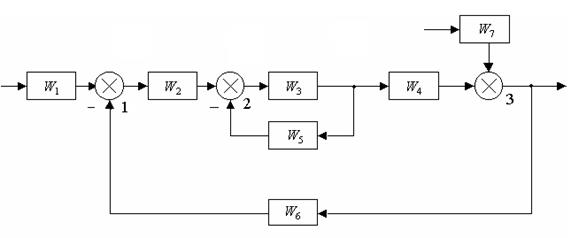1 Преобразуем местную отрицательную обратную связь звено с передаточной функцией W₃ охвачено обратной связью W₅ к одному звену с передаточной функцией: W₈ = W₃/(1 + W₃×W₅);

2 Преобразуем последовательно соединенные звенья W₂, W₈ и W₄ к одному звену
 с передаточной функцией: W₉ = W₂ W₃ W₄ / (1+W₃W₅);

3 Преобразуем обратную связь к звену с передаточной функцией: W₁₀ = W₁ (W₂ + W₃ + W₄)/ (1–W₁W₅(W₂ +W₃ + W₄));

4 Преобразуем последовательно соединенные звенья W₁₀ и W₆ к одному звену с передаточной функцией: W₁₁ = W₁W₆(W₂ +W₃+W₄)/(1–W₁W₅(W₂ +W₃ + W₄));

5. Перенесем сумматор 3 влево через звено W₉, добавляем к сумматору передаточную функцию звена в степени минус единица W₁₀ = W₇/W₉; Сумматор 3 переносим через сумматор 1 в начало схемы;

 (Ф3 – ЗТ)

5)  Используя правила структурных преобразований упростить структурную схему до одного звена с одной обратной связью, указать этапы преобразований

1 Преобразуем местную положительную обратную связь (звено с передаточной функцией W₁ охвачено обратной связью W₂, через сумматор 4) к одному звену с передаточной функцией: W₆ = W₁/(1 – W₁×W₂)

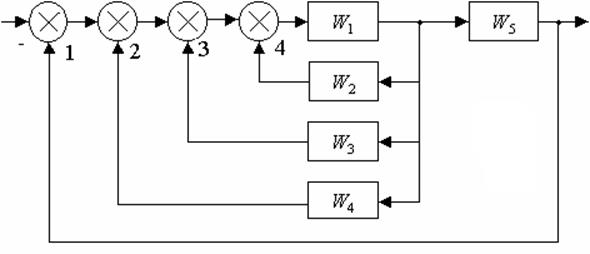2 Преобразуем местную положительную обратную связь (звено с передаточной функцией W₆ охвачено обратной связью W₃, через сумматор 3) к одному звену с передаточной функцией: W₇ = W₆/(1 – W₃×W₆);

3 Преобразуем местную положительную обратную связь (звено с передаточной функцией W₇ охвачено обратной связью W₄, через сумматор 2) к одному звену с передаточной функцией: W₈ = W₇/(1 – W₄×W₇);

;

4 Преобразуем последовательно соединенные звенья W₈ и W₅ к одному звену с передаточной функцией: W₉ = W₅W₈;

 (Ф3 – ЗТ)

6)  Используя правила структурных преобразований упростить структурную схему до одного звена с одной обратной связью, указать этапы преобразований

1 Преобразуем местную отрицательную обратную связь (звено с передаточной функцией W₄ охвачено обратной связью W₅, через сумматор 4) к одному звену с передаточной функцией: W₉ = W₄/(1 – W₄×W₅)

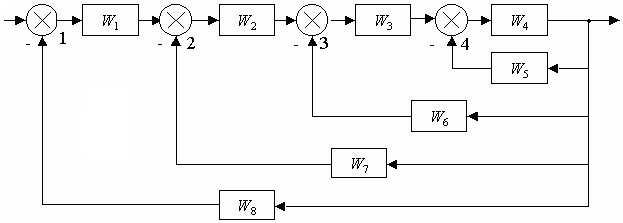2 Преобразуем местную отрицательную обратную связь (звено с передаточной функцией W₉ охвачено обратной связью W₆, через сумматор 3) к одному звену с передаточной функцией: W₁₀ = W₉/(1 – W₆×W₉);

3 Преобразуем местную отрицательную обратную связь (звено с передаточной функцией W₁₀ охвачено обратной связью W₂, через сумматор 2) к одному звену с передаточной функцией: W₁₁ = W₁₀/(1 – W₇×W₁₀);

4 Преобразуем последовательно соединенные звенья W₁ и W₁₁ к одному звену с передаточной функцией: W₁₂ = W₁W₁₁;

 (Ф3 – ЗТ)