Проектирование питающих электрических сетей энергосистем: Учебное пособие для курсового проектирования по дисциплине «Электропитающие системы и электрические сети», страница 10

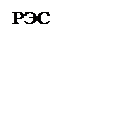
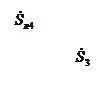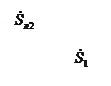Рис. 3.3. Схема для расчета послеаварийного режима кольцевой сети,

возникающего после отключения линии Л1

          Предварительный расчет потокораспределения в послеаварийных режимах производится аналогично нормальному режиму разомкнутой сети, то есть по первому закону Кирхгофа. Например, для режима, схема которого приведена на рис. 3.3, мощности определяются по следующим формулам:

узел 1:                                                     (3.18)

узел 2:                                             (3.19)

узел 3:                                             (3.20)

узел 4:                                             (3.21)

          В разомкнутой сети число послеаварийных режимов также равно числу линий. Однако часть линий либо все линии в такой сети являются двухцепными. Предполагается, что одновременное отключение обеих цепей двухцепной линии является маловероятным, так как эти цепи расположены на разных опорах. Поэтому в качестве послеаварийного режима рассматривается отключение только одной цепи двухцепной линии, а вторая цепь остается в работе. При этом конфигурация сети по сравнению с нормальным режимом не изменяется. Следовательно, потокораспределение также не изменяется и остается таким же, как в нормальном режиме. Однако последнее справедливо только для разомкнутых сетей.

          Например, в сети, изображенной на рис. 3.2 (все линии – двухцепные), могут возникать следующие послеаварийные режимы: первый режим – отключение одной цепи линии Л1; второй – отключение одной цепи линии Л2; третий – отключение одной цепи линии Л3; четвертый – отключение одной цепи линии Л4. Потокораспределение во всех этих режимах будет таким же, как в нормальном режиме, поэтому расчет для этих режимов проводить не требуется.

Однако если одна или более линий разомкнутой сети являются одноцепными, что может быть при наличии источника ограниченной мощности, то потокораспределение в режимах, возникающих при отключении этих линий, будет отличаться от нормального режима. Поэтому для таких режимов требуется произвести расчеты.

Результаты расчета потокораспределения в нормальном и всех послеаварийных режимах для обоих вариантов сетей целесообразно представить в виде таблицы.

Пример.

Продолжаем рассматривать пример, начатый в предыдущих разделах.

Определим длины линий. Длина каждой линии равна корню квадратному из суммы квадрата разности абсцисс и квадрата разности ординат точек, соединяемых линией.

Первый вариант сети (рис. 2.2).

Линия Л1 соединяет РЭС и подстанцию №1. Согласно исходным данным, координаты РЭС – 0, 0 км; координаты подстанции №1 – 0, 20 км. Тогда длина линии равна

 км.

          Линия Л2 соединяет подстанцию №1 и подстанцию №2, координаты которой равны 20, 40 км. Тогда

 км.

          Длины остальных линий определяются аналогично. Результаты их расчета сведены в таблицу 3.1.

Второй вариант сети (рис. 2.3).

Длины линий определяются таким же образом, как и в первом варианте сети. Результаты расчета сведены в таблицу 3.1.

Таблица 3.1. Длины линий

Далее рассчитаем нагрузки потребителей.

Для потребителя №1 задано P₁ = 15 МВт и cosφ₁ = 0,65. Тогда модуль полной мощности, реактивная мощность и комплекс полной мощности потребителя №1 соответственно равны

 МВА,

  Мвар,

 МВА.

Результаты расчета остальных нагрузок сведем в таблицу 3.2.

Таблица 3.2. Расчет нагрузок потребителей