Приведем пример определения центра массы тела методом разделения его на отдельные тела, центры масс которых известны.
Пример 1. Определить координаты центра массы однородной пластины (рис.9). Размеры заданы в миллиметрах на рисунке 9.
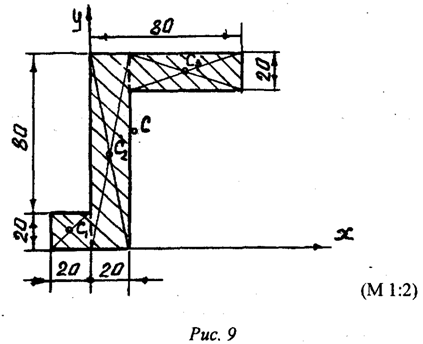
Решение: Показываем оси координат ![]() и
и
![]() . Разбиваем пластину на части,
которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим
диагонали, точки пересечения которых
. Разбиваем пластину на части,
которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим
диагонали, точки пересечения которых ![]() и
и![]() определяют положения центров массы
каждого прямоугольника. В принятой системе координат несложно найти значения
координат этих точек. А именно:
определяют положения центров массы
каждого прямоугольника. В принятой системе координат несложно найти значения
координат этих точек. А именно:
![]() (-1;
1),
(-1;
1), ![]() (1;5),
(1;5),![]() (5;9).
Площади каждого тела соответственно равны:
(5;9).
Площади каждого тела соответственно равны:
![]() ;
; ![]() ;
;
![]() .
.
Площадь всей пластины равна:
![]() .
.
Для определения координат центра массы заданной пластины применяем выражения (21). Подставим значения всех известных величин в данном уравнении, получим
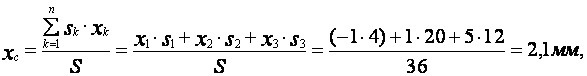
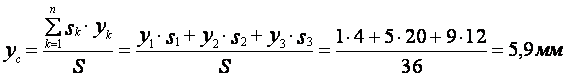 .
.
Согласно полученных значений координат центра массы пластины укажем точку С на рисунке. Как видно, центр массы (геометрическая точка) пластины находится за ее пределами.
Способ дополнения. Этот способ есть частичным случаем способа разделения. Он может применяться к телам, которые имеют вырезы (пустоты). Причем, без вырезанной части, положение центра массы тела известно. Рассмотрим например применение такого метода.
Пример 2. Определить положение центра массы веса круглой
пластины радиусом R, в которой есть вырез радиусом r (рис.10). Расстояние ![]() .
.
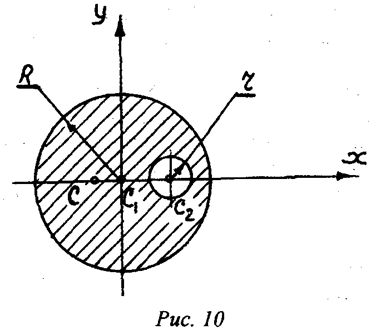
Решение: Как видим, из рис.10 центр массы пластины лежит на
оси симметрии пластины, то есть на прямой ![]() ,
поскольку эта прямая есть осью симметрии. Таким образом, для определения
положения центра массы этой пластины необходимо определить только одну
координату
,
поскольку эта прямая есть осью симметрии. Таким образом, для определения
положения центра массы этой пластины необходимо определить только одну
координату ![]() , поскольку вторая координата
, поскольку вторая координата ![]() будет расположена на оси симметрии и
уравновешивает нулевые. Покажем оси координат
будет расположена на оси симметрии и
уравновешивает нулевые. Покажем оси координат ![]() ,
, ![]() . Примем, что
пластина складывается из двух тел – из полного круга (как будто без выреза) и
тела, которое как будто выполнено с вырезом. В принятой системе координат
координаты
. Примем, что
пластина складывается из двух тел – из полного круга (как будто без выреза) и
тела, которое как будто выполнено с вырезом. В принятой системе координат
координаты ![]() для указанных тел будут равны:
для указанных тел будут равны: ![]() .Площади тел равны:
.Площади тел равны: ![]() ;
; ![]() .
Общая площадь всего тела будет равна разнице между площадями первого и
второго тела, а именно
.
Общая площадь всего тела будет равна разнице между площадями первого и
второго тела, а именно
![]() .
.
Теперь, для определения неизвестной координаты центра массы заданной пластины применяем первое уравнение выражения (21). Подставим значения всех известных величин в это уравнение, получаем
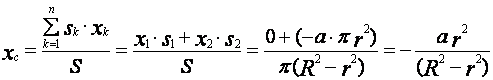 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.