Определение координат центра тяжести плоских фигур (лабораторная работа), страница 6

Определение координат центра массы тела, объема, площади, линии

в интегральной форме

         До этого было рассмотрено определение координат центра массы однородных тел, в которых удельный вес  - это величина постоянная (). Теперь рассмотрим определение этих координат для неоднородного твердого тела.

         Пусть есть неоднородное тело произвольной формы (рис.6). Разобьем его на  элементарных элементов и выделим из них один k-й элемент. Обозначим его массу через . Пусть , и  - координаты центра массы k-того элемента. Подставим в формулы координат центра массы тела (13) значения массы элемента , получим

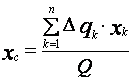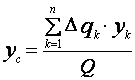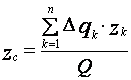, , .                  (26)

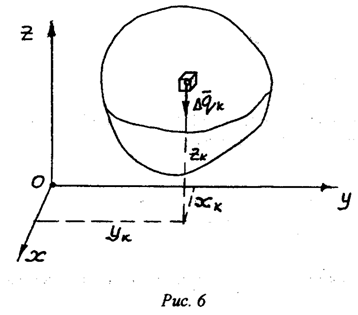
         Точка приложения силы  находится в середине элемента. Для точного нахождения точек приложения этих сил необходимо, чтобы объем каждого элемента n стремился к нулю, а число элементов неограниченно увеличивалось, то есть n∞. А поэтому необходимо, чтобы суммы выражений (26) рассматривались в пределах границ. А именно

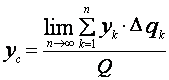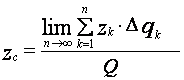, , ,  (27)

где  Q - масса всего тела.

         Как известно, границы пределов, которые есть в числителе выражений (27), не зависят от выбора точек приложения сил  и представляют собой интегралы, которые распространены по всему объему тела, то есть

,

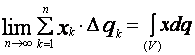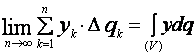,                              (28)

.

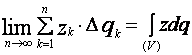Теперь, если подставить выражения (28) в (27), окончательно получаем координаты центра массы неоднородного тела в интегральной форме

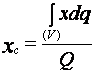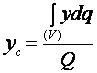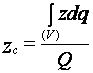, , .                       (29)

Для однородного тела можно определить координаты центра массы объема тела в интегральной форме. Если учесть, что

 =,                                    (30)

где   – элемент объема тела,

а

Q=,                                          (31)

где   – объем тела,

то, подставляя (30) и (31) в (29) и сокращая на ,  получаем

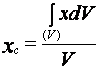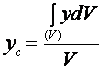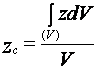, , .                   (32)

         Из формул (32) следует, что положение центра массы однородного тела не зависит от физических особенностей его материала, а зависит только от геометрической формы и размеров тела.