Определение координат центра тяжести плоских фигур (лабораторная работа), страница 3

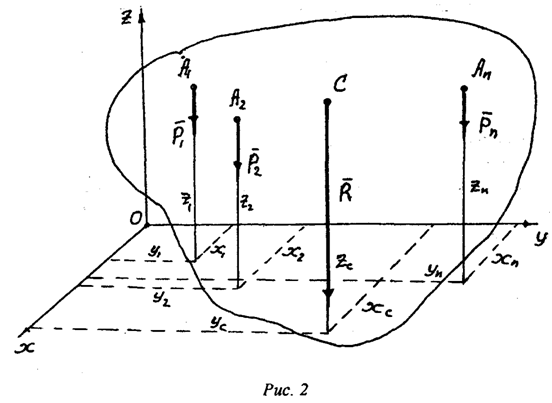
         Обозначим в принятой системе координат координаты точек приложения сил  (,,), (,,), (, ,), …, (,,) и С(,,) – точка приложения равнодействующей. Найдем моменты всех сил  относительно оси у. Поскольку =, то  по теореме Вариньона()=,

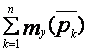 поэтому

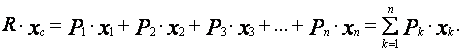 (5)

         Отсюда координата  будет равна

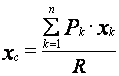                                                         .                              (6)

Точно так же найдем моменты всех сил относительно оси .

Получаем -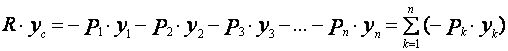.  (7)

Отсюда координата  будет равна

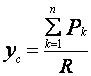.                                     (8)

         Далее повернем все силы на один и тот же угол в одну сторону

 ( например, на угол 90 перпендикулярно к плоскости ). Положение точки С, как известно, при повороте тела не меняется. Найдем теперь моменты всех сил относительно оси .

         Получаем

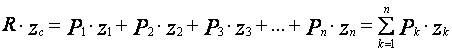.    (9)

Отсюда координата  будет равна

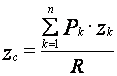.                             (10)

         Таким образом, окончательно получаем формулу для  координат центра параллельных сил

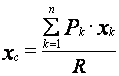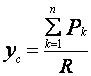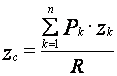,   ,    .               (11)     

Центр массы тела, объема, площади, линии

         На любую часть  тела, которая находится вблизи поверхности Земли, действует сила,  направленная  вертикально вниз,  которая имеет название сила тяжести (веса). Если считать радиус Земли достаточно большим (6,4 тыс. км), то для тел, размеры которых в сравнении с этим радиусом очень малы, силы тяжести, которые действуют на частицы тела, можно считать параллельными. Они сохраняют свою собственную величину, несмотря на какие-либо повороты тела.