Определение координат центра тяжести плоских фигур (лабораторная работа), страница 4

         Пусть есть тело, которое можно условно поделить на несколько частей (рис.3). На каждую часть действует сила массы ,,,…,соответственно. Как  видим, это есть система параллельных сил, для которой можно найти равнодействующую. Применяя (4), найдем эту равнодействующую.

         Она равна

+++…+=.               (12)

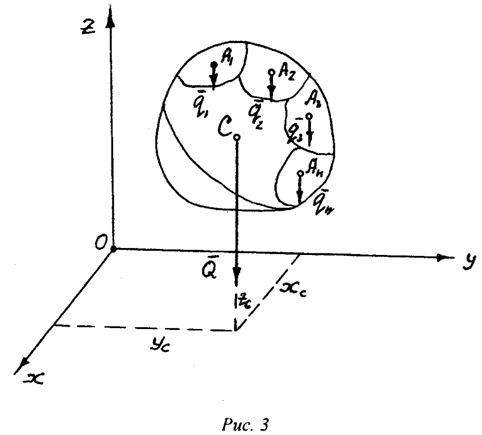
         При любом повороте тела силы  остаются   приложены к тем же точкам и параллельны между собой. Изменяется только направление этих сил по отношению к телу. А поэтому равнодействующая  будет при любом повороте тела приложена в точке, которая есть центром параллельных сил. Эта точка имеет название центр массы тела.

         Таким образом, центр массы тела – это точка,  неизменно связанная с этим телом, в котором приложена  сила тяжести, и которая не меняет своего положения при повороте тела на некоторый угол.

         Найдем координаты центра массы как центра параллельных сил ,,,…, и подставим в выражение (11), получим

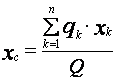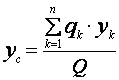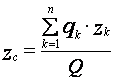,   , ,            (13)

где  ,  и - координаты приложения  силы массы частиц тела .

         Если тело однородное, то масса каждой части пропорциональна ее объему, а именно

=,                                  (14)

где    - коэффициент массы (масса единицы объема),

- объем части тела.

Для всего тела масса определяется по такой формуле

Q=V,                                       (15)

где    V – объем тела.

         Теперь подставим (14) и (15) в (13). При этом в числителе удельный вес - , как постоянный  множитель, выносится за скобки и сокращается с , который есть в  знаменателе. А именно:

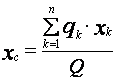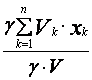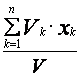==.            (16)

Аналогично поступаем и при определении двух других координат. Окончательно имеем координаты центра массы объема

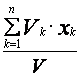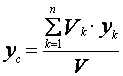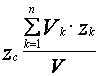,   ,   .         (17)

         Как видно, центр массы однородного тела зависит только от его геометрической формы. И, поэтому выражение (17) называется центр массы объема.