Определение координат центра тяжести плоских фигур (лабораторная работа), страница 10

         Общая длина дуги АВ будет равна

      .                                              (42)

         Подставим эти значения в первое уравнение (39). При этом интеграл, который находится в числителе данного выражения, должен быть определен по всей длине дуги.

Получаем

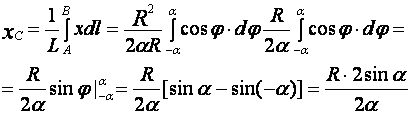       (43)

         Таким образом, координата  будет равна

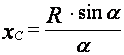.                                  (44)

2.  Центр массы треугольника

Имеем треугольник, вершины которого в принятой системе координат  определяются точками с координатами  и (рис.13).

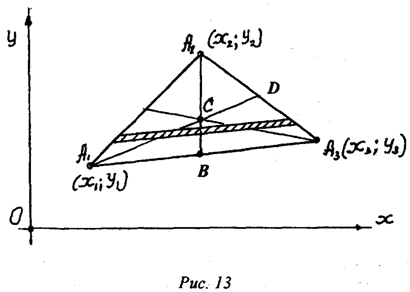
         Если провести достаточное количество прямых, которые параллельны основанию , то вся фигура треугольника будет разбита на полосы бесконечно малой ширины,  центры масс которых будут лежать посередине каждой из полученных полос. И поэтому центр массы треугольника будет лежать на его медиане . Далее, если провести линии, параллельные другой стороне треугольника, то и в этом случае центр массы будет лежать на его второй медиане . Также можно построить в треугольнике и третью медиану. Таким образом, вполне вероятно, что центр массы треугольника С будет размещен в точке пересечения трех его медиан, при этом =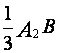; СД=.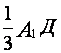

         Найдем координаты центра массы. Из аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями

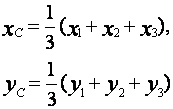                                        (45)

где   - координаты вершин треугольника.

3.  Центр массы сектора

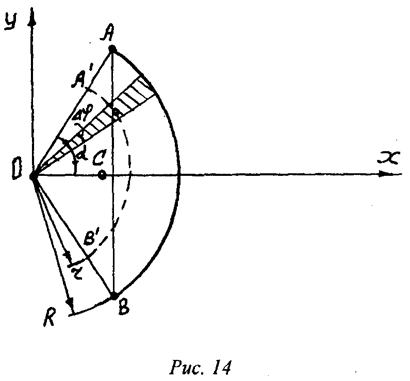
         Рассмотрим круговой сектор ОАВ радиусом R, центральный угол которого равен 2 радиан (рис.14). Центр массы сектора, вполне вероятно, лежит на оси его симметрии, то есть на биссектрисе угла АОВ. Эту биссектрису примем за ось  и найдем на этой оси  точку С.  Разобьем  площадь сектора на бесконечное число элементарных секторов с центральными углами . Будем рассматривать каждый сектор как угольник с основанием  и высотой R. Центры массы каждого такого треугольника лежат на расстоянии 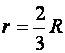 от центра сектора. Таким образом, центры массы каждого треугольника расположены на дуге . Если  стремится к нулю (), то достаточно найти центр массы дуги . Согласно формулы (44) центр массы дуги  будет равен

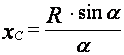.                              (46)

         Тогда, считая, что 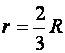, получим