Теперь, если
рассмотреть тело, которое представляет собой пластину (рис.4) толщина которой h , то координата 
центра ее массы будет равна =
.
Для определения двух других координат 
, 
используем уравнение (13). Пластину
необходимо разбить на несколько частей, которые имеют собственную массу. Дальше
считаем, что масса каждой части пластины будет равна
, (18)
где
- удельный вес (вес единицы объема),
h - толщина пластины,
- площадь части пластины.
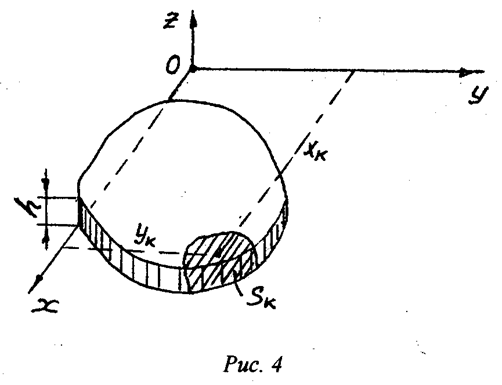
Масса этой пластины будет равна
Q=
=
, (19)
где s – площадь пластины.
Теперь необходимо
подставить (18) и (19) в первые два уравнения (13). Сделаем это сначала для
координаты , получим
=
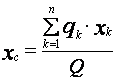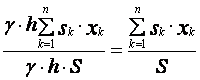. (20)
Таким же образом
найдем значения и другой координаты . Окончательно
имеем координаты центра массы тонкой пластины в таком виде
,=
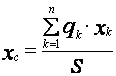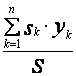. (21)
Точка, координаты которой определяются по формуле (21), имеет название центра массы площади.
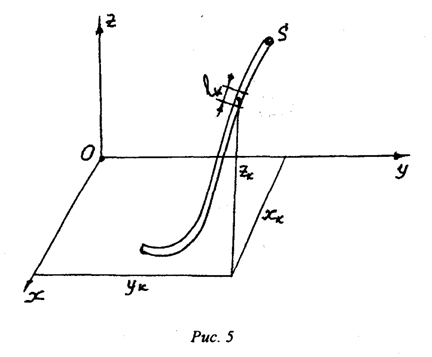
Теперь определим координаты центра массы линии. Это может быть например, проволока малого диаметра (рис.5). Как и в предыдущих случаях, сначала определим массу каждой части линии и массу всей ее длины. Вес части линии будет равен
=
=
, (22)
где -
удельный вес (вес единицы объему),
S - площадь поперечного сечения линии,
- длина части линии.
Масса всей длины линии будет равна
Q=
=
, (23)
где L-общая длина линии.
Теперь подставим
значения (22) и (23) в (13) и определим сначала координату . Она будет равна
=
=
.
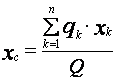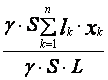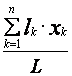(24)
Таким же образом определим две другие координаты центра массы линии.
Таким образом,
=, 
,
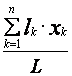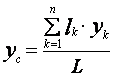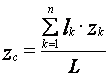. (25)
Как видно из формул (25), координаты массы линии зависят только от формы линии и общей ее длины, но не зависят от способа разделения линии на отдельные части.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.