Определение координат центра тяжести плоских фигур (лабораторная работа), страница 7

         Точно так в интегральной форме можно определить координаты центра массы площади.  Найдем положение центра массы однородной пластины, которая имеет постоянную толщину h (рис.7). Координата  центра массы будет равна 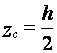. Определим другие две координаты. Также выделим в пластине элемент объема  в форме элементарной призмы с основанием  dS, высотою h и ребрами, которые перпендикулярны площади симметрии пластины. Элементарный объем будет равен

,                                   (33)

а полный объем пластины будет

  ,                                      (34)

где  S – площадь пластины.

         Подставим (33) и (34) в первые два уравнения   (32), получим

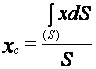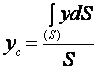, .                        (35)

         Формулы (35) есть формулами, которые определяют координаты центра массы площади.

         В формулах (35) в числителях стоят выражения статических моментов площади относительно координатных осей  и , а именно

, .                        (36)

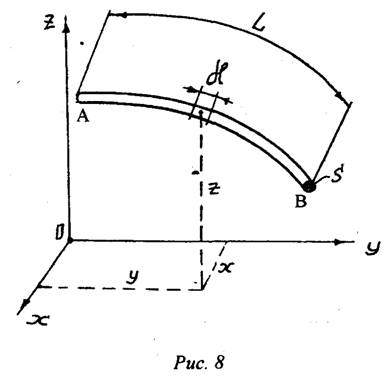
          Таким же образом найдем координаты центра массы линии в интегральной форме. Для этого возьмем однородное тело, например в виде  проволоки АВ с постоянной площадью поперечного сечения S и длиною L (рис.8). Выделим в проволоке элемент  полного объема. Если элемент имеет форму цилиндра  с основанием S и высотою dl, то элементарный объем будет равен

.                                    (37)

         Полный объем всего тела, который рассматривается, будет равен

.                                        (38)

         Теперь, подставив (37) и (38) в (32), найдем координаты центра массы данного тела

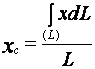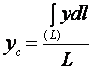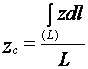, , .                        (39)

         Интегралы, которые стоят в числителях выражений (39), имеют название криволинейных интегралов. Как видим, положение центра массы однородного тела в виде проволоки не зависит от его поперечных размеров. А поэтому формулы (39) определяют координаты центра массы линии.

Способы определения  координат центра массы тела

Существуют несколько способов определения  координат центра массы тела. Среди них разделяют способы: симметрии, разделения и дополнения, экспериментальные способы.

         Рассмотрим последовательно эти способы.

Способ симметрии. Если однородное тело имеет площадь, ось или центр симметрии, то его центр массы лежит соответственно в площади симметрии, или на оси симметрии, или в центре симметрии.

         Так, центры массы однородных симметричных тел таких , как кольца, прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые имеют центр симметрии, лежат в геометрическом  центре (центре симметрии) этих тел.

Способ разделения. Если тело можно разбить на бесконечное число таких частей, для каждой из которых положение центра массы известно, то координаты центра массы всего тела определяют непосредственно по формулам (13), (17), (21) и (25). При этом количество слагаемых в каждом числителе указанных выражений будет равняться количеству частей, на которые разбито тело.