Проектирование и расчет одиночного обыкновенного стрелочного перевода, страница 7

          при деревянных шпалах, смешанном скрепле­нии – 3I_Г;

          при деревянных шпалах, раздельном скреп­лении - 4 I_Г;

          при железобетонных шпалах - 5I_Г,

           где I - момент инерции поперечного сечения рель­са в горизонтальной плоскости ( прил. 3);

погонное сопротивление поперечному перемещению рельсошпальной решетки, кг/см;

 то же, продольному перемещению, кг/см;

 длина волны искривления путевой решетки при выб­росе, см;

наименьший радиус кривой на участке укладки бес­стыкового пути, см.

 При эпюре шпал 1840 шт/км  P = 13 кг/см, q = 8,5 кг/см, при эпюре шпал 2000 шт/км Р = 14 кг/см, q = 9,0 кг/см. Критические силы по формулам  и  определяются подбором. Задаются значением Р и вычисляют .Под­ставляя полученное значение  и (которым задавались) в формулу для вычисления . Таким образом, получают несколько значений и , по которым строят два графика (рис. 4) точка пересечения которых дает ис­комую величину  и - общие корни уравнений . Полученные значения проверяют и, если расхождение не превышает 2% то расчет закан­чивают.

          Расчет проводим для кривого участка пути и сводим его таблицу.

Допускаемая максимальная температурная сила при этом определяется с учетом коэффициента запаса, равного 1,2.

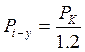
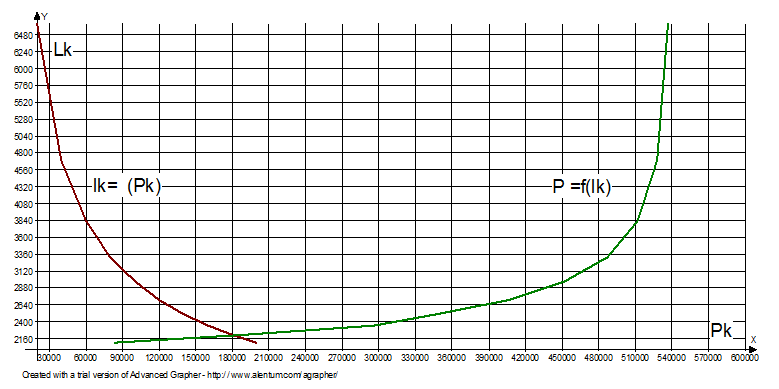
Рис. 4. Графическое определение  и по формулам К.Н.Мищенко

Коэффициент запаса вводится по тем соображениям, что при­веденная методика включает характеристики пути Р,  q,  ве­личины которых определяются опытным путем.

2.2.2 Расчет по формуле С.П.Першина

В 1959 г. С.П.Перщин предложил метод расчета с учетом начальных неровностей и переменной жесткости рельсошпальной рамы (по линейному закону в зависимости от угла поворота рель­сов относительно шпал). Он кроме того, ввел в расчет перемен­ные (по линейному закону в зависимости от величины смещения) сопротивления рельсошпальной решетки поперечному сдвигу. На основании энергетических условий равновесия С.П.Першин вывел формулу для определения закритической силы N_З -, приводящей к выбросу пути в горизонтальной плоскости. В результате ряда упрощений и многовариантных численных расчетов формула приоб­рела следующий вид

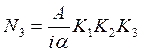
где  - параметры, зависящие от типа рельса и плана ли­нии;

- средний уклон начальной неровности в плане, при­нимается равным 2-3 (для прямых -  = 2%, для кривых -  = 2,5-3,0%);

 коэффициент, зависящий от сопротивления Q бал­ласта поперечному смещению шпалы, определяется по интерполяционному графику (рис. 5). При этом следует учитывать, что сопротивление сдвигу же­лезобетонной шпалы поперек оси пути при не засы­панных шпальных ящиках Q = 3,70 кН, при нор­мальном профиле балластной призмы Q =4,70 кН, при засыпанных концах шпал Q =6,0 кН, при уп­лотнении призмы поездами и чистом балласте Q = 8,5-9,0 кН.

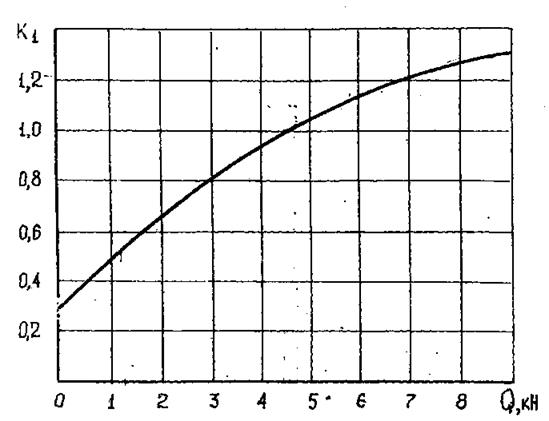
Рис. 5. Кривая изменения коэффициента К₁ в зависимости от сопротивления       

            балласта смещению в нем шпал

Сопротивление деревянных шпал при:

·  слабом уплотнении ЭШП Q = 4,4 кН;

·   уплотнении путевыми машинами Q = 6,0 кН;

·  после обкатки пути поездами Q = 8,0-9,0 кН.

 Как правило, рельсовые плети бесстыкового пути укладыва­ют в путь после стабилизации балластной призмы, поэтому реко­мендуется принимать расчетное значение К₁ = 1,2-1,3 как для деревянных, так и для железобетонных шпал.

K₂ - коэффициент, зависящий от эпюры шпал, равный 0,9; 1,0 и 1,08 при эпюре шпал, соответственно 1600, 1840 и 2000 шт/км;