





1) Функции, суперпозиция функций, обратная функция.
Опр.1. Даны ![]() .Если каждому элементу
.Если каждому элементу ![]() поставить по некоторому правилу
поставить по некоторому правилу ![]() ставится в соответствие единственный эл-т
ставится в соответствие единственный эл-т ![]() , то говорят, что на мн-ве X задана функция со значением в мн-ве Y и обозначают
, то говорят, что на мн-ве X задана функция со значением в мн-ве Y и обозначают ![]() .
.
Х – называется О.О.Ф. ![]() и
называется значением функции на Эл-те Х и мн-во всех значений функции
называется множеством значений функции и обознач.
и
называется значением функции на Эл-те Х и мн-во всех значений функции
называется множеством значений функции и обознач. ![]() .
.
Опр.2. Пусть ![]() ,
, ![]() . Функция
. Функция ![]() назыв.
суперпозицией функций
назыв.
суперпозицией функций ![]() и
и ![]() если
если ![]() выполнено
выполнено ![]() и
обозначается
и
обозначается ![]() ,т.е.
,т.е. ![]() .
.
Опр.3.Дана функция ![]() . Если
. Если ![]() , то функция назыв. взаимнооднозначной.
, то функция назыв. взаимнооднозначной.
Опр.4. Дана ф. ![]() . Пусть ф.
взаимнооднозначная, тогда
. Пусть ф.
взаимнооднозначная, тогда ![]() существует существует
единственный
существует существует
единственный ![]() из О.О.Ф., такой что
из О.О.Ф., такой что ![]() . Обозначим
. Обозначим ![]() .Таким
образом, на множестве Х задается функция
.Таким
образом, на множестве Х задается функция ![]() ,
которая называется обратной функцией
,
которая называется обратной функцией ![]() .
.
Замеч.1.Обратные функции существуют только у взаимнооднозначных. Применяется следующая терминология:
1) если О.О.Ф. Х есть N, то функция называется последовательностью.![]()
![]() -
- ![]() -член последовательности.
-член последовательности.
2) ![]() тогда
тогда ![]() называется
функцией одного вещественного переменного.
называется
функцией одного вещественного переменного.
2) Ограниченность и монотонность функций одного вещественного переменного.
Функция ![]() называется ограниченной,
если множество значений этой функции – ограниченное мн-во или если сущ-ет М>0
такое, что
называется ограниченной,
если множество значений этой функции – ограниченное мн-во или если сущ-ет М>0
такое, что ![]()
![]()
Опр. 6.
![]() называется:
называется:
1) не убывающей(возрастающей) если ![]()
2) не возрастающей(убывающей) если ![]()
3) если ф. одна из 4 типов, то её наз-ют монотонной.
4) если возрастающая или убывающая, то строго монотонная.
Т1. Пусть ![]() строго монотонная, тогда
у неё существует обратная и обратная – строго монотонная того же типа.
строго монотонная, тогда
у неё существует обратная и обратная – строго монотонная того же типа.
Док-во: докажем для возрастающей функции. Пусть ![]() . Если
. Если ![]() , то
, то
![]() . Значит ф. взаимнооднознач. (по
опр.3) и у неё есть обратная (по опр.4). Докажем, что
. Значит ф. взаимнооднознач. (по
опр.3) и у неё есть обратная (по опр.4). Докажем, что ![]() возрастающая.(от
противного).
возрастающая.(от
противного).
Пусть ![]() .
. ![]()
![]() . Противоречие с тем, что
. Противоречие с тем, что ![]()
![]()
![]() .
Значит
.
Значит ![]() возрастающая по опр.6.
возрастающая по опр.6.
Замеч.2. Обратная функция существует не только у строгомонотонных.
3) Окрестность точки, предельные изолированные точки, предел функции и последовательность.
Опр.1. Пусть ![]() . Множество
. Множество ![]() =
=![]() =
=![]() =
=
=![]() - это
- это ![]() окрестность
точки
окрестность
точки ![]() .
.
![]() =
= ![]() -
проколотая
-
проколотая ![]() окрестность точки
окрестность точки ![]() .
.
Опр.2. Точка ![]() называется предельной
точкой мн-ва Х если
называется предельной
точкой мн-ва Х если ![]()
![]() . Точка
. Точка ![]() называется изолированной точкой мн-ва
называется изолированной точкой мн-ва ![]() , если
, если ![]() и сущ-ет
и сущ-ет
![]() такое что
такое что ![]() .
.
Опр.3. Дана ф. ![]() ,
,![]() ,
,
![]() - предельная точка Х. Число или точка В
называется пределом функции f в точке
- предельная точка Х. Число или точка В
называется пределом функции f в точке
![]() или при
или при ![]() если для
любого
если для
любого ![]() существует
существует ![]() такое,
что
такое,
что ![]() из
из ![]() выполняется
выполняется
![]() . Это обозначается:
. Это обозначается: ![]() или
или
![]() .
.
Замеч.1. ![]()
Опр. 4. Число или точка b называется пределом последовательности ![]() если
если ![]() такое,
что
такое,
что ![]() выполняется
выполняется ![]() .
Обозначается
.
Обозначается ![]() или
или ![]()
4) Единственность предела.
Если существует предел функции в т.а, то этот предел единственный.
Док-во: пусть пределов 2, т.е. ![]()
![]() . по опр.3 пар.3 для этого
. по опр.3 пар.3 для этого ![]() сущ-ет
сущ-ет ![]() такое
что
такое
что ![]()
![]() .По опр.3пар.3 для
этого же
.По опр.3пар.3 для
этого же ![]() сущ-ет
сущ-ет ![]() такое,
что
такое,
что ![]()
![]()
![]()
![]() . Очевидно, что
. Очевидно, что ![]() ,
,
![]() . Тогда
. Тогда ![]()
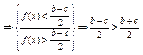 -противоречие, значит b=c и предел – единственный.
-противоречие, значит b=c и предел – единственный.
5) Ограниченность функции имеющ. Предел. Теоремы о стабилизации знака и о определенном переходе в неравенство.
Т2
(об ограниченности функции имеющей
предел) Если сущ. ![]() , то функция f ограничена в некоторой проколотой
окрестности точки а.
, то функция f ограничена в некоторой проколотой
окрестности точки а.
Т3 (о стабилизации знака)Если ![]() ,тогда f(x)>0
в некоторой точка проколотой окрестности точки а.
,тогда f(x)>0
в некоторой точка проколотой окрестности точки а.
Т4 (о предельном переходе к неравенству)
Пусть
существует 2 предела ![]()
и
пусть в некоторой проколотой окрестности точки а, ![]()
Зам.1.Если f(x)<g(x), то ![]()
![]()
![]()
____________________________________________
6) Теорема о пределе сжатой функции.
Пусть
![]() и пусть в некоторой проколотой окрестности
точки
и пусть в некоторой проколотой окрестности
точки ![]() ,
,
![]() . Тогда
. Тогда ![]() .
.
Док-во:
возьмём ![]() , по опр.3 пар.3 сущ-ет
, по опр.3 пар.3 сущ-ет ![]() , такое что
, такое что ![]() по
опр.3 пар.3 для того же
по
опр.3 пар.3 для того же ![]() сущ-ет
сущ-ет ![]()
![]()
![]()
по
усл. сущ-ет ![]() , такая что
, такая что ![]()
Возьмём,
![]() .
. ![]()
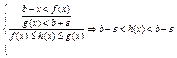
итак,
т.к. ![]() мы брали произвольно, то
мы брали произвольно, то ![]() сущ-ет
сущ-ет ![]() , такое
что
, такое
что ![]() выполняется нер-во, то по опр.3 пар.3
сущ-ет
выполняется нер-во, то по опр.3 пар.3
сущ-ет ![]() .
.
7) Предел суммы разности и частность
Т1 Пусть ![]() ,тогда
,тогда ![]()
На
практике ![]()
Доказательство (приведем для суммы):
Возьмем
![]() по опред.3 ( Дана функция
по опред.3 ( Дана функция ![]() , a-предельная
точка множества X. Число или точка b
называется пределом функции f в точке a,
или при x стремящимся к а, если для
, a-предельная
точка множества X. Число или точка b
называется пределом функции f в точке a,
или при x стремящимся к а, если для ![]() , такое
что
, такое
что ![]() выпол.
выпол. ![]() ) для
) для![]()
![]() по опред.3(приведенному
выше)
по опред.3(приведенному
выше)
![]()
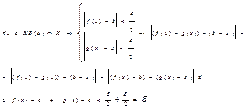
![]() сущ-ет
сущ-ет
![]()
По
определению 3 мы придем ![]() ч.т.д.
ч.т.д.
Т3Пусть![]() ;
;![]() ;
;
![]()
____________________________________________
8) Предел произведения
Лемма1 Пусть f-функция ограничена в некоторой проколотой окрестности
точки а. Пусть ![]() ,тогда
,тогда![]()
Доказательство:
Поусловию![]() Возьмем
Возьмем ![]() по по
оред.3 ( Дана функция
по по
оред.3 ( Дана функция ![]() , a-предельная
точка множества X. Число или точка b
называется пределом функции f в точке a,
или при x стремящимся к а, если для
, a-предельная
точка множества X. Число или точка b
называется пределом функции f в точке a,
или при x стремящимся к а, если для ![]() , такое
что
, такое
что ![]() выпол.
выпол.![]() )
)
для
![]()
![]() . Возьмем
. Возьмем
![]() ,тогда
,тогда![]()
![]() по опред3(см выше)
по опред3(см выше)
![]()
Т2![]()
Док-во:
![]()
По
теореме 1. по лемме1 (разность стремится к нулю) ![]()
Следствие1 Пусть
![]()
![]()
Док-во:
![]()
____________________________________________
9) предел суперпозиции
Т4 ![]() Пусть
Пусть![]()
![]() в некоторой проколотой окрестности точки.
Пусть
в некоторой проколотой окрестности точки.
Пусть![]() тогда
тогда![]()
Доказательство:![]()
По
опр. предела для ![]() т.к.
т.к. 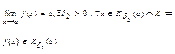 по
усл.
по
усл.
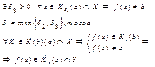
Подставив
в * вместо ![]() Итак
Итак ![]()
По
опред.![]()
Т5
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.