Множества и операции над ними. Отображения. Модуль и его свойства. Формула Тейлора с остаточным членов в форме Лагранжа и Пеано. Разложение функций по формуле Тейлора

1. Множества и операции над ними.

Множество – совокупность объектов выделяемых нами по каким-то признакам. (X)

Элемент множества – объекты составляющие множество. (x)

xX

Отношение включения: Множество А содержится в множестве В, если каждый эл-т множества А является и элементом множества В. АВ

Два множества называются равными (А=В), если выполняются 2 включения: АВ, ВА

Подмножество множества А – любое множество содержащееся в А. АА

В называется собственным подмножество А, если В содержится в А. Если В≠А, В – несобственное подмножество А.

Операции над множествами:

- Объединение множеств – такое множество, которое состоит из всех элементов, по крайней мере принадлежащих одному из множеств А и В. А  В

-  Пересечение множеств – множество состоящее из элементов, принадлежащих и множ. А и множ. В. АВ

- Пустое множество – если множество не содержит ни одного элемента.

- Непересекающиеся множества – если их пересечение пустое множество.

- Разность 2х множеств – множеств состоящее из эл-тов А, но не приналежащее множеству В. А\В

- Дополнением к множеству А называется множество состоящее из элементов, не принадлежащих можеству А. СА

- Произведением множеств Х и Y называется множество из упорядоченных пар (x,y), где х€Х, у€ Y.

XY, XY≠ YX

Свойства:

1) ССА=А

2) АВ= В  А

     АВ= ВА

3) А(ВC)= (АВ)C

     А (ВC)= (АВ) C

4) А(ВC)= (АВ)(АC)

    А (ВC)= (АВ)(АC)

Множества:

N – множество натуральных чисел N={1, 2, 3…}

Z – множество целых чисел {0, +-1,+-2…}

R – множество действительных(вещественных) чисел

NZR

2. Отображения

Если между X и Y соответствие и элемент x сопоставляется y(x€X–>y€Y), то говорят, что задана ф-ция f, зависимости Х и Y(f:X–>Y или y=f(x))

f:X–>Y

- сюръективное, если Y_f=Y (f: отображ. множество Х на все множество Y)

- инъективное, если x₁≠x₂ => f(x₁)≠f(x₂) (разные элементы множества Х не могут одновременно сопоставляться с одним и тем же элементом Y)

- биективное, если оно одновременно является сюръективным и инъективным.

f:X–>Y; АX тогда образом А при отображении f, называется множество ВY такое, что для любого элемента b€И существует a€A такой, что f(a)=b. f(A) – образ множества А

f:X–>Y; ВY тогда прообразом В при отображении f, называется множество АХ такое, что любой элемент а€А имеет значение b=f(a)€B

f^-1(B) – прообраз множества В

Обратное отображение:

Пусть дано биективное отображение

f:X->Y. Тогда по определению биекции для каждого y€Y существует в точности один x€X, такой что f(x) = y. Таким образом построена функция y€Y->x€X. Эта функция называется обратной к F и обозначается F ⁻¹

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.Топологические структуры. Классификация точек множества.

Даны множества Х и Т. Топологическая структура множества X, если для его эл-тов выполняется 2 аксиомы: 1)объединение любого числа эл-тов из Т. 2)конечное пересечение эл-тов из Т также принадлежит Т.

множество входящее в семейство Т – открытое множество.

Тривиальная топология: T={ ,X}

Дискретная топология: Т – множество всех подмножеств множества Х.

А называется замкнутым в Х, если его дополнение X\A из аксиом.

Любое конечное пересечение замкнутых множеств является замкнутым множеством. Любое конечное объединение замкнутых множеств явл. замк. множ.

Классификация точек множества.

Предельная точка Х – точка x, кот обладает cв-вом: любая окрестность точки х содержит точки множ-ва Х отличные от х.

Изолированная точка Х – точка, у которой есть окрестность, кот. не содержит точки множ-ва Х за исключ. самой точки х.

Внешняя точка Х – точка, кот не € множ-ву Х и имеется окрестность этой точки не перечек. с Х.

clX=C(intX): cl – замыкание, int – внутренность.

5.Модуль и его свойства.

Модуль вещественного числа x есть расстояние от x до нуля.

Более точно: Модуль x есть неотрицательное число, обозначаемое |x|, определяемое следующим образом: если x ≥ 0, то |x|=x; если x < 0, то |x| = −x. Для абсолютной величины имеют место следующие соотношения:

|a| ≥ 0

|a| = 0 тогда и только тогда, когда a = 0.

|ab| = |a||b|

Модуль действ.  числа и его свойства.

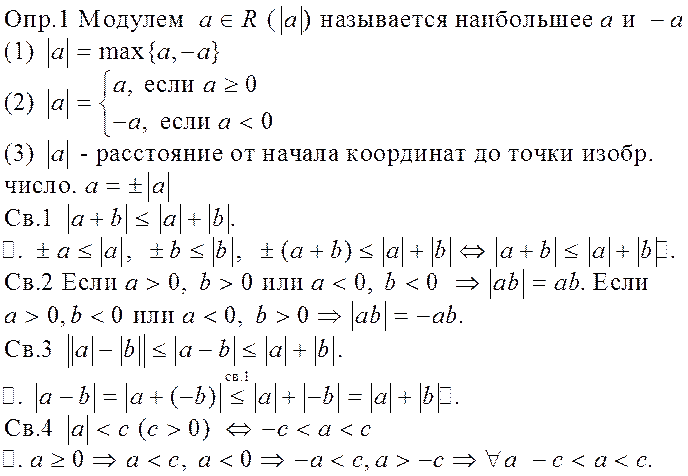
Модуль и основные неравенства.

            x; x>0

|х|=      0; x=0

            -x; x<0

 

|x|<h   Û -h<x<h           |x|>hÛ      x>h

 h>0                                                  x<-h

1)  " а,b Î R: |a±b|£|a|+|b|

2)  " а,b Î R: |a-b|³||a|-|b||

Можно рассматривать окрестности бесконечности:

О_ε(+¥)={xÎR:x>ε}    (//////////        x

                           ε>0               ε

О_ε(-¥)={xÎR:x<-ε}  ///////////)  ·   x

   ε>0                         -ε  0

О_ε(¥)={xÎR:|x|>ε}        \\\\\\)   _·    (//////    x

         x>ε;x<-ε                                       -ε                    ε

1. Предел числовой последовательности.

если каждому натуральному n поставлено число х_n, то говорят что задана числовая последовательность х₁,x₂…x_n={x_n}

O:Числ. посл. называется занумерованная совокупность чисел рассматриваемая в порядке возрастания. Общий эл-т последовательности является функцией от n. x_n=f(n)

O: Последовательность {x_n} – ограниченная, если существует