Функции, суперпозиция функций, обратная функция. Ограниченность и монотонность функций одного вещественного переменного. Единственность предела. Понятие приближенного значения корня уравнений. Метод половинного деления нахождения приближенного корня, страница 3

.По определению 3( существует .Для любого

Существует >0. Для любого

. Тогда для любого

.

16)Непрерывность функции в точке, односторонняя непрерывность

Определение1

Говорят, что функция непрерывна в точке , и если изолированная точка X

или предельная точка X и предел

Если функция непрерывна в каждой точке X, то  говорят f  непрерывна на множестве Х.

Теорема1 Пусть функция fg непрерывна в, тогда

будут  непрерывны в точке .

Доказательство:

Если точка  изолирована то fg непрерывна в точкетогда

Теорема доказана.

Теорема2 . Пусть функция f  непрерывна  в точке  , а функция g непрерывна ,тогда суперпозиция gºf непрерывна в точке .

Доказательство:

Если -изолированная точка, по определению1(этого раздела)1 пункт. Пусть -предельная точка

по теореме 5(

)

предел при  

Суперпозиция непрерывна по пункту 1 опред1(этого раздела) теорема доказана.

Определение2

1)Функция f называется непрерывной слева в точке,если  изолированная точка или еслипредельная слева и

2)называется непрерывной справа в точке если изолированная точка илипредельная справа и

Теорема3 Пустьпредельное справа и слева f непрерывна в точкеи тогда и только тогда, когда f одновременно непрерывно и справа и слева.

Доказательство:

f непрерывна в точке 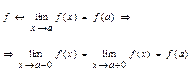,теорема1(Пусть а – предельная слева и справа точка Х. Тогда , тогда и только тогда, когда  и .

)это равносильно тому, что пределы слева и справа одинаковы по опред.

17)Точки разрыва функции, классификация этих точек

Определение3точканазывается точкой разрыва функции f если функции (обл.опред.)и не является точкой непрерывности функции f или , но является предельной точкой множества Х(в первом случае -предельная точка)

Определение4(классификация точек разрыва), точка , точка разрыва функции f  называется :

1)точкой устранимого разрыва, если сущ. конечный предел

2)Точкой разрыва первого рода , если 3)точкой разрыва второго рода, если она не является точкой разрыва первых двух типов, т.е.хотя бы один из односторонних пределов не сущ. или бесконечен.

Дальше должно быь два графика и параграфа10

Замечание1 Пусть точка устранимого разрыва. Рассмотрим ____________________________________________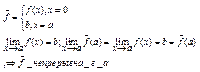

18) Свойства функций, непрерывных на отрезке.

Опр. 1

. Число называется наибольшим значением функции на множестве .

Число называется меньшим значением функции на множестве .

Теор. 1(Вейерштрасса). Пусть  непрерывна на, тогда ограничена наи сущ-ют и в кот.

Теор. 2.(Больцано-Коши о сущ-ии корня). Пусть непрерывна на отрезке и пусть на концах отрезка принимает значения разных знаков, т.е. .

Тогда сущ-ет точка , такая что

Теорема 3.( Больцано-Коши о промежуточных значениях). Пусть непрерывна на отрезке и пусть дано число , тогда сущ-ет , такое что

Док-во: Пусть D=m,тогда по т.1(вверху) сущ-ет, такое что . ,тогдп сущ-ет , такое что .

Пусть . Рассмотрим функцию . По т.1(см. выше) сущ-ют и сущ-ет

Пусть для опред-ти . Рассмотрим на отрезке . Она непрерывна, как разность непрерывных функций

. удовлетворяет теореме 2 на отрезке и значит сущ-ет С , такое что , тогда и след-но .

19

) Дифференцируемость функций.Производная.Непрерывность дифференцируемых функций.

Как мы помним,- это любая функция, такая что .

Определение 1. -предельная точка . Функция называется дифференцируемой в точке , если существует А, такое что

Функция обозначается наз-ся дифференциалом в т. .

Пример 1.

Опр. 2

Если сущ-ет конечный предел , то он называется производной функции в т. и обозначается , т.е.

Предл. 2. Если функция дифференцируема в точке , то она непрерывна в точке (Обратное неверно!)

Док-во:по опр.1(см.выше)

20)Связь дифференцируемости функций и существование производной.

Функция дифференцируема в т. тогда и только тогда, когда сущ-ет , то справедлива формула (ф-ла Тейлора I порядка).

Док-во: 1)пусть дифференцируема в т. , тогда по опр.1: и

сущ-ет .