____________________________________________
10)Предел и монотонность
Т1
1)Неубывающая, ограниченная сверху последовательность име6ет конечный предел
2)Невозрастающая, ограниченная снизу последовательность имеет конечный предел
Доказательство(случая1):
Т.к.![]() (послед.) ограничена сверху, то по
предложению 2 (Пусть множество Х ограничено сверху тогда для него сущ. Ед.
точная верхняя граница. Пусть множество Х огр. Сущ., тогда для него сущ. И ед.
точная нижняя граница. (без доказательства))
(послед.) ограничена сверху, то по
предложению 2 (Пусть множество Х ограничено сверху тогда для него сущ. Ед.
точная верхняя граница. Пусть множество Х огр. Сущ., тогда для него сущ. И ед.
точная нижняя граница. (без доказательства))![]() докажем,
что
докажем,
что ![]() .Возьмем
.Возьмем ![]() , т.к.
А- верхняя граница, то
, т.к.
А- верхняя граница, то![]()
![]() -не является верхней границей,
-не является верхней границей,![]()
![]() .Т.к.
.Т.к.![]() -наиб.
То
-наиб.
То
![]()
Т.к.![]() бралось произвольно, получаем:
бралось произвольно, получаем:
![]()
![]()
![]()
11)Число е
Лемма 1(неравенство Бернулли)
Для любого ![]() и для любого
и для любого ![]()
![]()
Теорема 2
Существует конечный предел ![]()
Доказательство:
![]()
![]() для любого
для любого ![]()
![]() и значит,
и значит, ![]() ограничено
снизу.
ограничено
снизу.
Рассмотрим ![]()
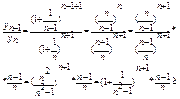
![]()
![]() -не
возрастающая. По теореме 1 п.7 (неубывающая (невозрастающая) ограниченная
сверху(снизу) последовательность имеет конечный предел) существует конечный
предел
-не
возрастающая. По теореме 1 п.7 (неубывающая (невозрастающая) ограниченная
сверху(снизу) последовательность имеет конечный предел) существует конечный
предел ![]() (
(![]() )
)
![]() и
значит существует конечный
и
значит существует конечный ![]()
Определение 1
Числом ![]() называется
называется
![]()
![]()
Следствие 1.
1. ![]()
2.
![]()
12)Сравнение предельного
поведения функции, операции с символами о,0,![]()
Определение 1.
![]() .
. ![]() - предельная точка
- предельная точка ![]()
1)если ![]() ,то
пишут
,то
пишут ![]() при
при ![]() (
(![]() )
)
2)если ![]() ,то
пишут
,то
пишут ![]() при
при ![]() (
(![]() )
)
3)если ![]() ограничено
в некоторой проколотой окрестности точки
ограничено
в некоторой проколотой окрестности точки ![]() , то
пишут
, то
пишут ![]() при
при ![]() (
(![]() )
)
Пример:
1)![]()
![]() при
при ![]()
![]()
2) ![]()
для любого ![]() при
при ![]()
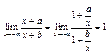
3) ![]()
![]() при
при ![]() для
любого
для
любого ![]()
![]() -ограниченная
функция
-ограниченная
функция
Определение 2.
Если ![]() ,
то функция называется бесконечно малой при
,
то функция называется бесконечно малой при ![]()
Пусть ![]() и
и
![]() бесконечно малые при
бесконечно малые при ![]() ,
, ![]() при
при ![]() , то говорят, что
, то говорят, что ![]() -
бесконечно малая более высокого порядка, чем
-
бесконечно малая более высокого порядка, чем ![]() при
при ![]() .
.
Если ![]() при
при
![]() , то
, то ![]() и
и ![]() называются эквивалентными бесконечно малыми
при
называются эквивалентными бесконечно малыми
при ![]() .
.
Замечание 1.
1) ![]() -
бесконечно малая при
-
бесконечно малая при ![]() ,
, ![]()
![]()
![]()
![]()
2) ![]() ограничено
в некоторой проколотой окрестности точки
ограничено
в некоторой проколотой окрестности точки ![]() и по
опр. следует, что
и по
опр. следует, что ![]()
![]()
Предложение 1.
Пусть ![]() ,
,
![]() при
при ![]() . Тогда:
. Тогда:
1) если ![]() , то
, то ![]()
2) если ![]() , то
, то ![]()
Док-во(1 пункт):
![]()
Замечание 2
1) ![]()
![]()
2) предл.1 означает, что
произв. и част. мы можем заменить функцией на функции, связанные с исх. значком
![]() . В сумме, разности и степени этого делать
НЕЛЬЗЯ!
. В сумме, разности и степени этого делать
НЕЛЬЗЯ! ![]()
![]()
![]()
![]()
Предложение 2
1) Пусть ![]()
![]()
Тогда для любого ![]() ,
, ![]()
![]()
![]()
2) Пусть ![]() ,
, ![]()
![]()
![]() при
при ![]() (
(![]() )
)
3) ![]()
![]()
Тогда ![]() при
при
![]() (
(![]() )
)
4) ![]() при
при ![]()
![]() при
при ![]()
Док-во:
1)![]()
![]() при
при![]()
2) ![]() (по
лемме 1 пар. 5(пусть
(по
лемме 1 пар. 5(пусть ![]() ограничена в некоторой прокол.
окр-ти точки
ограничена в некоторой прокол.
окр-ти точки ![]() и пусть
и пусть ![]() , тогда
существует
, тогда
существует ![]() )
)![]() при
при ![]()
3) ![]() при
при ![]()
4) ![]() при
при ![]()
__________________________________________
13)Предел в расширенном множестве веществ числе R(c чертой), понятие неопределенности.
Определение 3.
Пусть ![]()
![]()
![]() :
: ![]()
![]()
![]() -
предельная точка Х.
-
предельная точка Х.![]() -называется
пределом
-называется
пределом ![]() в точке а или при
в точке а или при ![]()
Тогда ![]() ,
,
![]() для любого
для любого ![]()
![]() Определение
4Говорят, что
Определение
4Говорят, что ![]() если
если
![]() Говорят, что
Говорят, что ![]() если
если ![]()
Замечание 1
Если ![]() или
или
![]() , то
, то ![]() При
этом, обратное не верно!Предложение 1
При
этом, обратное не верно!Предложение 1
Пусть ![]() Тогда
Тогда
![]() Замечание 2.Во множестве
Замечание 2.Во множестве ![]() остаются справедливыми все теоремы об
операциях с пределами если эти операции определены в
остаются справедливыми все теоремы об
операциях с пределами если эти операции определены в ![]() .
В противном случае говорят, что предел представляет собой неопределенность и
указывают её тип.
.
В противном случае говорят, что предел представляет собой неопределенность и
указывают её тип.
14)Односторонние окрестности, предельные точки и пределы.
Определение 1.
Пусть ![]()
Множества ![]() и
и ![]()
![]() называются
соответственно, левой и правой
называются
соответственно, левой и правой ![]() - окрестностями точки
- окрестностями точки ![]() .
.
Очевидно, что ![]()
Определение 2.
Точка ![]() называется предельной слева
(справа) точкой множества Х, если пересечение любой её левой (правой)
называется предельной слева
(справа) точкой множества Х, если пересечение любой её левой (правой) ![]() - окрестности с Х не пусто.
- окрестности с Х не пусто.
Определение 3.
![]()
1. Пусть а - предельная слева точка Х. Число b называется пределом слева функции f в точке а, если для любого ![]() > 0, существует
> 0, существует ![]() >0
такое, что для любого
>0
такое, что для любого ![]()
Обозначение предела слева:
![]() или
или ![]()
2. Пусть а - предельная справа точка Х. Число b называется пределом справа функции f в точке а, если для любого ![]() > 0, существует
> 0, существует ![]() >0
такое, что для любого
>0
такое, что для любого ![]()
Обозначение предела справа:
![]() или
или ![]()
15)Связь предела и односторонних пределов
Теорема 1.
Пусть а – предельная слева и
справа точка Х. Тогда ![]() , тогда и только тогда, когда
, тогда и только тогда, когда ![]() и
и ![]() .
.
Доказательство:
1)![]()
Тогда для любого ![]() существует
существует ![]() , такое
что для любого
, такое
что для любого ![]() .Для любого
.Для любого ![]()
Для любого ![]() . Для любого
. Для любого ![]() .
.
2) ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.