значит f и g непрерывны в т. ![]() и т.к.
по п.2 f и g
дифференц. в каждой точке
и т.к.
по п.2 f и g
дифференц. в каждой точке ![]() , то f и g непрерывнына всем
, то f и g непрерывнына всем ![]() (по
пред. 2 пар. 12)
(по
пред. 2 пар. 12)
Пусть ![]() (в
ост. случ. аналогично)
(в
ост. случ. аналогично)
Возьмём ![]() и рассмотр. f и g на
отр.
и рассмотр. f и g на
отр. ![]() . На нем f и g удовл.
усл. т. 2 пар.15(Коши) и значит сущ-ет с,
. На нем f и g удовл.
усл. т. 2 пар.15(Коши) и значит сущ-ет с,![]() , что
, что ![]()
![]() . По т.о пределе сжатой
ф. (т. 5 пар. 4) при
. По т.о пределе сжатой
ф. (т. 5 пар. 4) при ![]()
![]()
![]()
Замеч.1.
1) ![]() -
правило Лопиталя раскрытия неопределенности
-
правило Лопиталя раскрытия неопределенности ![]() .
.
2) правило остается
справедливым если ![]() ,
, ![]()
![]() и
наз-ся прав. Лопиталя раскр. неопред.
и
наз-ся прав. Лопиталя раскр. неопред. ![]() .
.
3) также справедл. если ![]()
29)Вторая (дважды) дифф. функции.
Опр1![]()
![]() -предельная точка Х, если
-предельная точка Х, если![]() , такие что
, такие что ![]()
![]() , то функция f называется
дважды дифф. в точке
, то функция f называется
дважды дифф. в точке ![]()
Опр2 Пусть функция f дифф. в каждой точке окрестности![]() , тогда в этой окрестности можно
рассмотреть функцию f
, тогда в этой окрестности можно
рассмотреть функцию f![]() , если
эта функция имеет произвольную в точке
, если
эта функция имеет произвольную в точке![]() , то эта
производная называется второй производной функции f в точке
, то эта
производная называется второй производной функции f в точке ![]() и обознач.
и обознач.![]() либо
либо![]() либо
либо ![]() , т.е.
, т.е. ![]() .
.
Т1 ![]() если
если![]() ,то f дважды дифф.в
,то f дважды дифф.в![]() и справедлива ф-ла:
и справедлива ф-ла:![]()
(Формула Тейлора второго порядка )
Док-во: Рассмотрим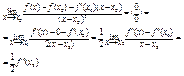
Введем функцию
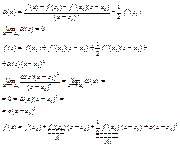
30)Критерии монотонности функции.
Т1 f непрерывна на [a;b] и дифф. в каждой точке (a;b), тогда:
1)f не убывает на [a;b], тогда
и только тогда, когда ![]() для любого х из (a;b)
для любого х из (a;b)
2)f не возрастает на отрезке [a;b] тогда
и только тогда, ![]()
3)если для любого,![]() то f возрастает на отрезке [a;b] (обратное
неверно)
то f возрастает на отрезке [a;b] (обратное
неверно)
4)если для ![]() ,то f убывает на отрезке [a;b]
,то f убывает на отрезке [a;b]
Док-во:
1)ч1 Пусть f не убывает на [a;b]. Возьмем![]() для
для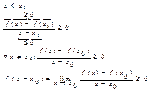
Т.К. ![]() БРАЛОСЬ
ПРОИЗВОЛЬНО, ТО
БРАЛОСЬ
ПРОИЗВОЛЬНО, ТО![]()
2)![]() возьмём
возьмём ![]() на отрезке
на отрезке ![]() f удовл. условию теоремы Лагранжа.
Сущ-ет
f удовл. условию теоремы Лагранжа.
Сущ-ет ![]()
![]() ,т.к.
,т.к. ![]() и
и![]() брались произвольно то f не убывает на отрезке [a;b]
брались произвольно то f не убывает на отрезке [a;b]
Зам.1. для пунктов 3 и 4 обратное не верно.
![]()
31)Критические точки. Необходимые условия экстремума.
Опр.1.![]() ,
,![]() . Т.
. Т. ![]() называют
критической точкой функции
называют
критической точкой функции ![]() , если она предельная
справа, но не слева для Х, или предельная слева, но не справа и
, если она предельная
справа, но не слева для Х, или предельная слева, но не справа и ![]() , либо
, либо ![]() не
существует. В частности, если
не
существует. В частности, если ![]() , то критическая точка
называется стационарной.
, то критическая точка
называется стационарной.
Т1.(необходимое усл.
экстремума).![]() . Если в т.
. Если в т. ![]() функция
достигает своего максимума, или наибольшего, или наименьшего значений, то
функция
достигает своего максимума, или наибольшего, или наименьшего значений, то ![]() -критическая точка функции.
-критическая точка функции.
Док-во: пусть ![]() -не критическая точка, тогда
-не критическая точка, тогда ![]() -предельная и справа и слева, в этой точке
сущ-ет
-предельная и справа и слева, в этой точке
сущ-ет ![]() и эта производная не равна нулю. По усл. и
след.1 пар. 14
и эта производная не равна нулю. По усл. и
след.1 пар. 14![]() .ПРОТИВОРЕЧИЕ
.ПРОТИВОРЕЧИЕ![]()
![]() -критическая точка
-критическая точка
![]()
32) Первое достаточное условие экстремума.
![]() ,
, ![]() пусть сущ-ет
пусть сущ-ет ![]() .
.
Пусть f дифференцируема
в каждой точке ![]() и пусть f непрерывна в т.
и пусть f непрерывна в т. ![]() , тогда:
, тогда:
1)если ![]()
![]() ,
, ![]()
![]() , то f достигает в т.
, то f достигает в т. ![]() max.
max.
2) если![]()
![]() ,
,![]()
![]() , то f
достигает в т.
, то f
достигает в т. ![]() min.
min.
3) ![]()
![]()
![]() либо
либо
![]() , то f не достигает в
т.
, то f не достигает в
т. ![]() экстремума.
экстремума.
Док-во: по предл. 2 пар.12 f –
непрерывна во всей ![]() окрестности(
окрестности(![]() ).Докажем 1:
).Докажем 1:
по т. 1 пар. 18 f –
возрастает на ![]() и убывает на
и убывает на ![]() , а потому для
, а потому для ![]()
![]() . По опр. 1 пар. 14 f
достигает в т.
. По опр. 1 пар. 14 f
достигает в т. ![]() - max.
- max.
33) Второе достаточное условие экстремума.
![]()
![]() и пусть сущ-ет
и пусть сущ-ет ![]() . Тогда:
. Тогда:
1)если ![]() >0,
то f достигает в т.
>0,
то f достигает в т. ![]() минимума.
минимума.
2) если ![]() <0, то f достигает в т.
<0, то f достигает в т.![]() макс.
макс.
Док-во: (1 пункт).по ф-ле Тейлора 2го порядка.
![]() =
=![]() . Рассмотрим:
. Рассмотрим: ![]()
=![]()
по т.3 пар. 4 сущ-ет ![]() , такое что
, такое что ![]()
![]()
![]()
![]() ,
по опр. 1 пар.14 f достигает
в т.
,
по опр. 1 пар.14 f достигает
в т. ![]() минимум.
минимум.
Зам1Если в усл.т.2 ![]() , то ничего сказать нельзя, требуется доп.
исследование.
, то ничего сказать нельзя, требуется доп.
исследование.
34)Выпуклость и вогнутость функции точки перегиба.
Опр1 ![]() Пусть функция f дифф. В точке
Пусть функция f дифф. В точке![]() , если
, если![]() такое,
что для
такое,
что для ![]() Выполняется
Выполняется ![]() то
функция f называется
выпуклой в точке
то
функция f называется
выпуклой в точке ![]()
![]()
![]()
, то f вогнутая в точке ![]() .
.
Т1 ![]()
![]()
1)тогда если![]() то f вогнута в точке
то f вогнута в точке![]()
2)если![]() то
f выпукла в точке
то
f выпукла в точке ![]()
Док-во:
2пункта) ф.Тейлора 2-го
порядка ![]()
Рассмотрим предел при![]()
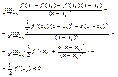
Пот3((о
стабилизации знака)Если ![]() ,тогда f(x)>0
в некоторой точка проколотой окрестности точки а.)
,тогда f(x)>0
в некоторой точка проколотой окрестности точки а.)
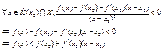
По
опр1 f выпукла в точке ![]() ч.т.д.
ч.т.д.
Опр2
![]() (предельное
и справа и слева) Пусть f дифф.
В точке
(предельное
и справа и слева) Пусть f дифф.
В точке ![]() .Если сущ.
.Если сущ. ![]() , такое
что
, такое
что
![]()
или
наоборот то![]() называется точкой перегиба функции f.
называется точкой перегиба функции f.
Т2![]() (
(![]() -предельная и справа и
слева для Х)Пусть
-предельная и справа и
слева для Х)Пусть ![]() , то по т1 f вогнуто в точке
, то по т1 f вогнуто в точке ![]() если
если![]() , то по
т1 f выпукло в точке
, то по
т1 f выпукло в точке ![]() противоречение с тем, что
противоречение с тем, что![]() -точка перегиба, значит
-точка перегиба, значит![]() ч.т.д.
ч.т.д.
35)Асимптоты графика функции
Опр1 ![]() пусть
пусть![]() предельная точка множества X. Если
хотя бы один из пределов
предельная точка множества X. Если
хотя бы один из пределов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.