2) пусть сущ-ет ![]() .
. ![]() .
. ![]() по опр.2.( Если сущ-ет конечный предел
по опр.2.( Если сущ-ет конечный предел ![]() , то он называется производной функции
, то он называется производной функции ![]() в т.
в т. ![]() и
обозначается
и
обозначается ![]() , т.е.
, т.е. ![]() )
)
![]() (умножим
обе части на
(умножим
обе части на ![]() )
)
![]()
![]()
По опр.1 ![]() дифференцируема в т.
дифференцируема в т. ![]()
Предложение 1. Пусть ![]() дифференцируема в т.
дифференцируема в т. ![]() .
.
Тогда ![]() .
По опр.1
.
По опр.1 ![]()
21) Касательная графику функций.
Опр.3.![]()
![]() . Прямая
. Прямая ![]() ,
проходящая через точку
,
проходящая через точку![]() графика функции f
называется касательной графику функции f в т.
графика функции f
называется касательной графику функции f в т. ![]() , если
, если ![]() .Из
опр. 3 и 1 следует, что касательная в т.
.Из
опр. 3 и 1 следует, что касательная в т. ![]() существует
тогда и только тогда, когда f – дифференцируема в т.
существует
тогда и только тогда, когда f – дифференцируема в т. ![]() . Из
теор. 1 следует, что Ур-е касательной имеет вид:
. Из
теор. 1 следует, что Ур-е касательной имеет вид: ![]() . Пусть
. Пусть
![]() - угол наклона касательной к оси абсцисс,
то из Ур-я касательной следует, что
- угол наклона касательной к оси абсцисс,
то из Ур-я касательной следует, что ![]() - геометрический смысл
производной.
- геометрический смысл
производной.
22)Дифференцируемость арифметический операций.
Т1![]()
1)Для
![]() с f дифф. В точке
с f дифф. В точке![]() и производная
и производная![]()
2)![]() дифф. В точке
дифф. В точке ![]() и
и![]()
3)![]() дифф. В точке
дифф. В точке ![]() и
и ![]()
4)при
![]() f/g дифф. В точке
f/g дифф. В точке ![]() и
и ![]()
Доказательство: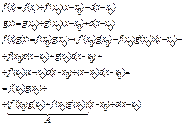
![]()
по
теореме 1 ![]()
23)Дифференцируемость . суперпозиции функции. Производные обратных тригонометрич. Функции.
Т2![]() Пусть функция f дифф.
В точке
Пусть функция f дифф.
В точке ![]() , а функция g дифф.в точке
, а функция g дифф.в точке ![]() , тогда суперпозиция дифф. В точке
, тогда суперпозиция дифф. В точке ![]()
![]() и
и ![]()
Доказательство:
По
усл. 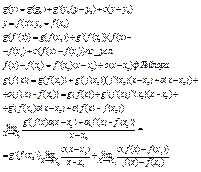
по опр.1 пар.12, то справедл.
ф-ла: ![]() ) , то
) , то
![]()
____________________________________________
24)Дифференцируемость обратной функции. Производные обратных тригонометрических функций.
Т3. Пусть ![]() имеет
обратную
имеет
обратную ![]() . Пусть f диффер. в т.
. Пусть f диффер. в т. ![]() . Пусть
. Пусть ![]() непрерывна
в
непрерывна
в ![]() . Тогда
. Тогда ![]() диффер.
в т.
диффер.
в т. ![]() и
и ![]()
Док-во:По усл. ![]()
Обозначим:![]() ,
,![]() ,
,
![]() . Подставим
. Подставим ![]()
Перенесём ![]() в лев.
часть и разделим на
в лев.
часть и разделим на ![]() :
:
![]()
![]()
![]()
при![]()
![]()
![]() =
=
=![]() =
=
=![]()
![]()
по т.1 пар12 ![]()
Пример.Пусть f=![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда по Т3:![]() =
=
=![]()
Пишут: ![]() ,
,![]()
![]() .
.
25.Экстремум функции . Теорема Ферма (14 параграф)
Опр.1. ![]()
Говорят,
что ф-я ![]() достигает в точке
достигает в точке ![]() :
:
1)max,
если ![]() предельная точка Х и
предельная точка Х и ![]() , такое что
для
, такое что
для![]()
2)min, если
![]() - предельная
т. Х и
- предельная
т. Х и ![]() ,
такое что
,
такое что ![]()
3)экстремум, если достигает max или min
4)
наибольшего значения, если ![]()
5)
наименьшее значение, если ![]()
В
первых трёх случаях точка ![]() называется точкой max, min, экстремума.
называется точкой max, min, экстремума.
Теорема
1.(Ферма) ![]()
Пусть
1)![]() предельная и
слева и справа 2)
предельная и
слева и справа 2)![]() такое что
такое что![]()
3)![]() тогда
тогда ![]()
Док-во.
Возьмём
![]() , тогда
, тогда ![]()
![]()
=![]()
![]()
(по
теор.4парагр.3(о предельном переходе в неравенство) Пусть существует 2
передела ![]() Пусть в некоторой проколотой окрестности
точки а,
Пусть в некоторой проколотой окрестности
точки а, ![]() )
)
![]()
![]() тогда
тогда ![]()
![]()
![]() .
.
Следствие 1. ![]()
Пусть
ф-я f в
точке ![]() предельная и слева и справа, достигает max или min или
наибольшее или наименьшее значение и пусть существует
предельная и слева и справа, достигает max или min или
наибольшее или наименьшее значение и пусть существует ![]() тогда
тогда ![]()
26)Теорема Ролля
Т.1(Ролля) Пусть функция f непрерывна на отрезке ![]() и дифф.
в каждой точке интервала (если она дифф. То она непрерывна) и пусть
и дифф.
в каждой точке интервала (если она дифф. То она непрерывна) и пусть![]()
Тогда![]()
Док-во: по т1(Вейштрасса Пусть
функция f непрерывна
на[a;b], тогда f огранич.
[a;b] и сущ. ![]() )
)
![]() 1случай:
m=M, тогда f-постоянная функция.
1случай:
m=M, тогда f-постоянная функция.![]()
2случай: m<M,
тогда одна из точек ![]() лежит внутри отрезка (a;b) (т.к.
если обе точки на концах, то m=M по
усл.)Ту точку внутри отрезка обозначим С по след1(Пусть fв точке
лежит внутри отрезка (a;b) (т.к.
если обе точки на концах, то m=M по
усл.)Ту точку внутри отрезка обозначим С по след1(Пусть fв точке![]() предельной и слева и справа, достигает мах
или min,или
наиболь. или наимень. значения. Пусть
предельной и слева и справа, достигает мах
или min,или
наиболь. или наимень. значения. Пусть![]() )
)![]()
Теорема доказана.
27)Теорема Коши и Лагранжа
Т2(Коши)Пусть функции f и g непрерывны на [a;b], и пусть f,g дифф. в каждой точке интервала (a;b). Пусть
![]()
Док-во:![]() т.к.
если g(a)=g(b) то по т.1(Пусть функция f
непрерывна на отрезке АВ и дифф. В каждой точке интервала (если она дифф. То
она непрерывна) и пусть
т.к.
если g(a)=g(b) то по т.1(Пусть функция f
непрерывна на отрезке АВ и дифф. В каждой точке интервала (если она дифф. То
она непрерывна) и пусть![]()
![]() )сущ.
)сущ.![]() ,такое что
,такое что![]() , что противоречит условию. Введем
функцию F(x)=f(x)-kg(x)
, что противоречит условию. Введем
функцию F(x)=f(x)-kg(x) ![]() F непрерывна на отрезке (a;b) как
разность непрерывной функции. F дифф.
в каждой точке отрезка (a;b) как разност дифф. функций. Подберем k так, чтобы F(a)=F(b)
F непрерывна на отрезке (a;b) как
разность непрерывной функции. F дифф.
в каждой точке отрезка (a;b) как разност дифф. функций. Подберем k так, чтобы F(a)=F(b)
F(a)-kg(a)=f(b)-kg(b)
K(g(b)-g(a))=f(b)-f(a)
![]() F удовл. Т.1(см
выше)
F удовл. Т.1(см
выше)![]()
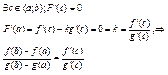
Т3.(Лагранжа)Пусть ![]() непрерывна на
непрерывна на ![]() и
диффер. на
и
диффер. на ![]() . Тогда
. Тогда ![]() ,
, ![]()
Док-во: Возьмем функцию g(x)=x, непрерывную на [a;b] и дифф. на (a;b) ,тогда по Т2(см выше)
![]()
____________________________________________
28) Правило Лопиталя. Раскрытие неопределенностей.
Т1. ![]()
![]()
1) ![]()
2) ![]() диффер.
в каждой т.
диффер.
в каждой т. ![]() и
и ![]()
![]()
3) ![]() , то
, то ![]() .
.
Док-во: доопределим функции f и g в т. ![]() положив
положив ![]()
![]()
![]() (по п.1)
(по п.1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.