Функции, суперпозиция функций, обратная функция. Ограниченность и монотонность функций одного вещественного переменного. Единственность предела. Понятие приближенного значения корня уравнений. Метод половинного деления нахождения приближенного корня, страница 6

,то прямаяназывается вертикальной асимптотой графика функции f, Очевидно, что если-вертик. Асимптота, то -точка разрыва второго рода.

Опр2 1)Пусть множество Х неограниченно сверху, если такие что

, то прямая y=kx+b называется правой наклонной асиптотой графика функции f.

2)Пусть множество Х не ограничено снизу, если такие что, то прямая y=kx+b называется левой накл. Асимптотой граф. Функции f,

Т1.Дана f:

1)пусть f не ограничено сверху, прямая y=kx+b –есть прав. накл.асимптота f тогда и т.т.,когда

2)то же самое, только левая и -бесконечность.

Док-во:

1)y=kx+b правая наклонная асимптота, тогда по опр2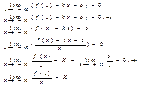

2)из второго предела, следует, что по опр2 y=kx+b 

36)Понятие приближенного значения корня уравнений. Метод половинного деления нахождения приближенного корня.

Опр. 1., число такое, что наз-ся корнем функции f(x) или корнем скалярного ур-я f(x)=0.

Опр.2. Числоназ-ся приближ. знач. корня с заданной точностью , если .

Задача нах-я приближ. корня состоит из 2х этапов:

1.Отделение корня. Нах-е на котором корень есть и притом 1. Для этого находят отрезок, на кот. f  дифференц. в каждой т.(следовательно, непрерывна). На концах этого отрезка функция принимает значение разность знаков, т.е. f(a)f(b)<0 и сохраняет знак на интервале (a;b), т.е. или , т.е. .

Тогда по т.2 пар.11 сущ-ет , такое что . Т.к. произв. сохраняет свой знак, то f либо возр. либо убыв. на и следовательно корень единственный.

2. Уточнение корня с заданной точностью - это нахождение отр. такого, что и . В этом случае, в кач. можно взять любую точку отр. . Обычно в кач. берут .

Метод половинного деления уточнения корня.

Пусть дан , в каждой точке кот. f – дифференцируема. f(a)f (b)<0, ., разделим этот отр. пополам точкой если , то мы нашли корень. Если , то из двух отр. выберем тот, на концах кот. функция принимает знач. разность знаков. Обозначим его его длина . Разделим отр. точкой пополам. Если

, то мы нашли корень. Если , то из двух отр. выберем тот, на концах кот. функция принимает знач. разность знаков. Обозначим его его длина .и далее повторяем процедуру. В итоге получ. посл-ть отрезков , на кот. есть ед. корень и длины кот. . Решим нер-во:, ,. В кач-ве n берем наим. нат. число, удовл. этому нер-ву. В итоге и

37)n-я дифференц. функции. Ф-ла Тейлора с остаточным членом в форме Пеано и в форму Лагранжа.

Опр.1.,. Если сущ-ют числа , такие что , то f называется n раз диффер. в т..

Опр.2. Пусть f (n-1) раз диффер. в нек. окр-ти т..Значит в этой окр-ти можно рассматр. как функц. Если эта ф. имеет произв. в т. , то эта произв. наз-ся n-ой произв. в т. .и обознач:,т.е.

Зам.1. n!=1*2*3*…*(n-1)n---n-факкториал

Очевидно, что n!=(n-1)!n  Удобно считать 0!=1

Удобно писать .

Теорема1. , -предельная точкаХ. Пусть сущ-ет n-я производная в т. , тогда f-n-раз диффер. в т.  и справедлива ф-ла:

Т2. Пусть f  (n+1)  дифференцируема в каждой т. (a;b) . Тогда сущ-ет с лежащее между ними такое что

38)Определение опред. интеграла. Теорема сущ-я.

Опр.1.Дан ,.Разобьем этот отрезок на n частей точками наз-ся разбиением на отр. (k=0,1,2,…,n-1) и обознач. П.Обознач..Числоназывается рангом разбиения П(макс. из длин отрезков разбиения). Возьмём на каждом отрезке точку . Полученное значение наз-ся разбиением с отмеченными точками и обозначается .

Опр.2. Пусть f ограничена на . Число

+называется интегральной суммой функции f по разбиению .

Опр.3.Число называется определенным интегралом от ограниченной функции f  по отрезку , если сущ-ет , такое что выполняется нер-во . Интеграл . f – интегральная функция. Если у f сущ-ет интеграл, то f наз-ся интегрируемой на .

Опр.4. Функция f наз-ся кусочно-непрерывной на Х если она ограничена и имеет конечное число точек разрыва, причем либо устранимых либо 1-ого рода.

Т1.(сущ-е).Если f кусочно-непрерывна на отрезке , то она интегрируема на .