


















Заметим, что при задании на одном и том же множестве Х различных метрик, из равенства нулю расстояния между элементами в одной метрике не следует равенства нулю расстояния в другой. Примеры подобных ситуаций будут приведены ниже.
2. r (xi, xj) = r (xj, xi).
Это утверждение называют аксиомой симметрии.
3. Для любых xi, xj, xk ÎХ r (xi, xk) £ r (xi, xj) + r (xj, xk).
Данное утверждение представляет собой аксиому треугольника, обобщающую на произвольные пространства хорошо известное из геометрии неравенство треугольника, в соответствии с которым любая сторона меньше суммы двух других сторон.
Обычно метрические пространства (Х, r) обозначаются одной буквой, определяемой типом множества, на котором определена метрика.
Рассмотрим примеры метрических пространств.
1.
Пусть для
элементов множества Х r (xi, xj) =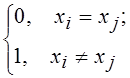 . Нетрудно
проверить, что все аксиомы метрики в этом случае выполняются. Такое метрическое
пространство называют пространством изолированных точек.
. Нетрудно
проверить, что все аксиомы метрики в этом случае выполняются. Такое метрическое
пространство называют пространством изолированных точек.
2.
Множество
действительных чисел R
при задании расстояния как ![]() , где x и y – любые числа, принадлежащие R, образует метрическое пространство R.
, где x и y – любые числа, принадлежащие R, образует метрическое пространство R.
3.
Будем называть
упорядоченную совокупность из n
действительных чисел ![]() n-мерным вектором
n-мерным вектором ![]() и
обозначать как
и
обозначать как ![]() =(
=(![]() ). Если
во вновь образованном множестве n-мерных векторов задать расстояние в виде
). Если
во вновь образованном множестве n-мерных векторов задать расстояние в виде 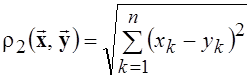 , то
получим n-мерное вещественное (действительное)
евклидово пространство
, то
получим n-мерное вещественное (действительное)
евклидово пространство ![]() . Аналогично определяется n-мерное комплексное пространство
. Аналогично определяется n-мерное комплексное пространство ![]() , для которого
, для которого 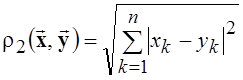 . Расстояние
. Расстояние ![]() является
частным случаем метрики
является
частным случаем метрики 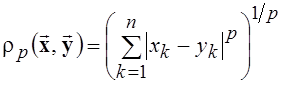 , где р – любое
число, не меньшее единицы. Часто удобно бывает рассматривать евклидово
расстояние с весом, определяемым вектором
, где р – любое
число, не меньшее единицы. Часто удобно бывает рассматривать евклидово
расстояние с весом, определяемым вектором ![]() с
неотрицательными компонентами
с
неотрицательными компонентами ![]() , т. е. рассматривать
, т. е. рассматривать 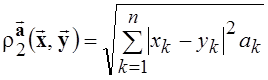 .
.
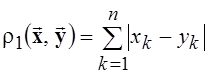 или метрику
или метрику Введенные метрические
пространства часто обозначают как ![]() при использовании
метрики
при использовании
метрики ![]() ,
, ![]() для
хэмминговой метрики
для
хэмминговой метрики ![]() и
и ![]() , если в
качестве метрики берется
, если в
качестве метрики берется ![]() .
.
4.
Евклидово пространство ![]() может быть обобщено на
случай бесконечномерных векторов
может быть обобщено на
случай бесконечномерных векторов ![]() = (
= (![]() , …), где
, …), где ![]() Î R и
выполняется условие
Î R и
выполняется условие 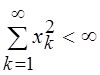 . Расстояние между векторами
данного пространства определяется формулой
. Расстояние между векторами
данного пространства определяется формулой 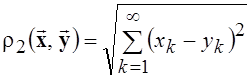 , а
оно само обозначается как l2.
, а
оно само обозначается как l2.
Если элементы векторов
бесконечномерного векторного пространства образуют ограниченные
последовательности, то можно обобщить метрику ![]() ,
определив
,
определив ![]() =
=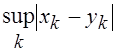 , где
, где ![]() – точная верхняя грань, обобщение понятия
– точная верхняя грань, обобщение понятия ![]() для бесконечных последовательностей.
для бесконечных последовательностей.
5.
Рассмотрим множество C[a, b] всех функций,
непрерывных на сегменте [a, b]
и определим метрику по аналогии с ![]() , т. е. расстояние между
любыми функциями f(t)
и g(t) из C[a, b]
зададим как
, т. е. расстояние между
любыми функциями f(t)
и g(t) из C[a, b]
зададим как ![]() . С помощью замены переменной
область определения функций может быть преобразована к сегменту [0, 1].
Метрическое пространство C[0,
1] обычно обозначается как С.
. С помощью замены переменной
область определения функций может быть преобразована к сегменту [0, 1].
Метрическое пространство C[0,
1] обычно обозначается как С.
6.
Если на множестве C[a,
b] ввести метрику по аналогии с ![]() ,
,
т. е. 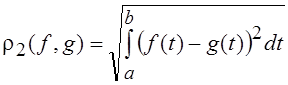 , то такое метрическое пространство называют
пространством непрерывных функций с квадратичной метрикой.
, то такое метрическое пространство называют
пространством непрерывных функций с квадратичной метрикой.
7.
Метрика r2(f,
g) может быть определена и на более широком
множестве функций, любая из которых удовлетворяет условию 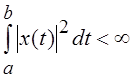 . Такое множество обозначается обычно как L2[a, b] и после введения
метрики
. Такое множество обозначается обычно как L2[a, b] и после введения
метрики ![]() превращается в метрическое пространство с
сохранением обозначения L2[a,
b].
превращается в метрическое пространство с
сохранением обозначения L2[a,
b].
Если речь идет о функциях,
определенных на всей оси (–¥, ¥) и удовлетворяющих условию 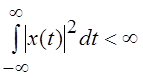 , то соответствующее метрическое пространство
обозначается как L2. Отметим, что элементами L2[a, b] или L2
могут быть как вещественные функции, так и функции, принимающие комплексные
значения.
, то соответствующее метрическое пространство
обозначается как L2. Отметим, что элементами L2[a, b] или L2
могут быть как вещественные функции, так и функции, принимающие комплексные
значения.
Как и для конечномерных пространств, часто используют евклидово расстояние с весом p(t), где p(t) – неотрицательная функция, и для каждой функции f(t) из L2[a, b]
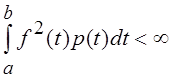 ,
,
т. е. расстояние между функциями f(t) и g(t) определяется как
![]() (f,
g) =
(f,
g) =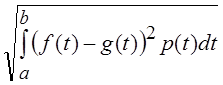 .
.
Выше были рассмотрены
метрики, определяемые для достаточно общих множеств. Для специфических множеств
могут быть введены свои способы определения расстояния. Так, для множества всех
пар вещественных чисел ![]() , лежащих на окружности
единичного радиуса с центром в начале координат и, следовательно,
удовлетворяющих условию x2 + y2 = 1, одна из возможных
метрик такова:
, лежащих на окружности
единичного радиуса с центром в начале координат и, следовательно,
удовлетворяющих условию x2 + y2 = 1, одна из возможных
метрик такова:
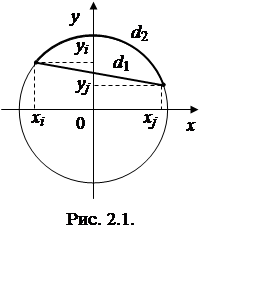
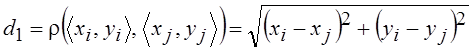 ,
,
т. е. представляет собой длину хорды, соединяющей точки xi, yi и xj, yj (см. рис. 2.1).
Примером специфической
метрики может также служить “метрика города”, заданная для множества,
состоящего из всех домов города и определяемая как минимальная длина пути между
домами по улицам города, т. е. 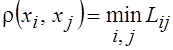 , где Lij – множество всех путей по улицам,
соединяющим дома xi и xj.
, где Lij – множество всех путей по улицам,
соединяющим дома xi и xj.
Введенные выше метрики
могут быть определены с соответствующими поправками и для множества комплексных
чисел, множества векторов с комплексными элементами, множества
комплекснозначных функций. Например, для множества комплекснозначных функций,
каждая из которых удовлетворяет условию 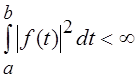 ,
евклидово расстояние
,
евклидово расстояние
r2(f, g) =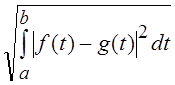 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.