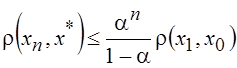Сходимость по метрике. Полнота метрических пространств. Принцип сжимающих отображений и его применение. Нормированные пространства, страница 3

,

где a определено в (2.1).

Принцип сжимающих отображений лежит в основе отыскания приближенных решений различных типов уравнений (алгебраических, дифференциальных, интегральных). Рассмотрим простейший пример использования принципа сжимающих отображений для решения уравнения x = f(x), к которому можно свести уравнение F(x) = 0, введя функцию  f(x) = x – lF(x), где
l – число, выбираемое так, чтобы отображение f  было бы сжимающим.

Будем считать, что функция f Î C[a, b] удовлетворяет условию Липшица  с константой k <1 и отображает сегмент [а, b] в себя. В этом случае f – сжимающее отображение и в соответствии с сформулированной выше теоремой имеет единственную неподвижную точку, являющуюся корнем уравнения x = f(x). Этот корень определяется как предел последовательности x₀, x₁ = f(x₀), x₂ = f(x₁), …, x_n = f(x_n–1), определяющей итерационную процедуру отыскания корня уравнения.

Если функция f(x) дифференцируема на сегменте [а, b],  и при этом
, то отображение, задаваемое f, является сжимающим с вытекающими из этого последствиями.

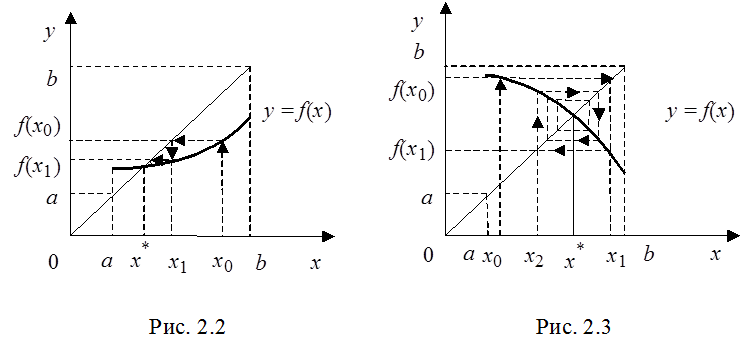
На рис. 2.2 и рис. 2.3 представлен ход последовательных приближений решения уравнения x = f(x) для случаев  (рис. 1.2) и  (рис. 2.3).

Число итераций зависит от начального приближения х₀, требуемой точности решения уравнения и значений производной в области итераций. Итерационная процедура заканчивается, если выполняется условие , где e – допустимая величина погрешности.

Рассмотрим конкретный пример. Пусть требуется определить постоянную времени T = RC интегрирующей RC- цепи, обеспечивающую при подаче на вход прямоугольного видеоимпульса с амплитудой U_m и длительностью t_и, а также белого шума со спектральной плотностью мощности 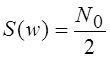 максимальное значение отношения сигнал/шум на выходе, понимая под ним отношение наибольшего значения сигнала на выходе к действующему значению выходного шума.

Наибольшее значение сигнала на выходе достигается к моменту окончания импульса и равно 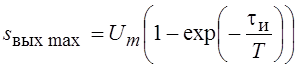. Действующее (среднеквадратическое) значение шума на выходе можно записать как 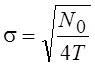. Тогда отношение сигнал/шум на выходе примет вид 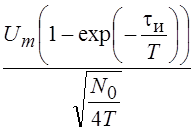. Вводя безразмерную переменную 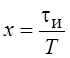, получим выражение, которое надо исследовать на экстремум: 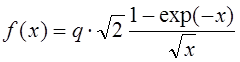, где 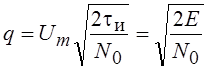 – максимально достижимое для данного сигнала и белого шума отношение сигнал/шум, получаемое с помощью согласованного фильтра. Исследуя функцию 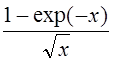 на экстремум, получим следующее уравнение для отыскания точки экстремума:

.

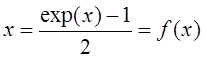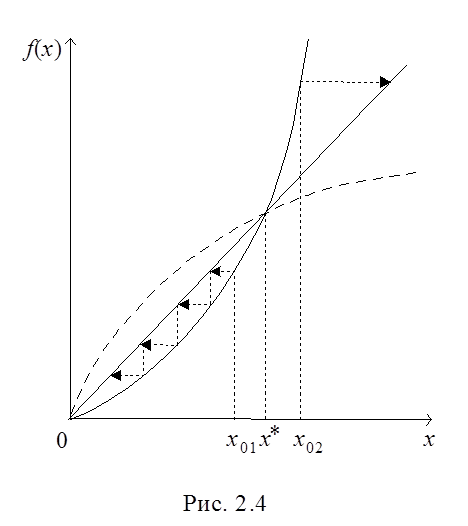На рис. 2.4. приведено графическое решение данного уравнения. Как видно, из-за невыполнения в окрестности корня х^* условия , итерационная процедура либо сходится к х = 0, что соответствует минимуму отношения сигнал/шум, равному нулю (убедиться в этом можно, раскрыв неопределенность f(0) по правилу Лопиталя), либо расходится, если начальное приближение х₀₂ взято правее корня х^*. Однако если перейти к уравнению x = f ^–1(x), где
 f ^–1(x) – функция, обратная 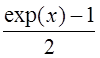, т. е.   f ^–1(x) = ln (2x + 1) (см. пунктирный график  на рис. 2.4), то условие существования неподвижной точки выполняется и, осуществляя несколько итерационных шагов, получим с приемлемой точностью значение х^* = х_opt @ 1.2. Этому решению соответствует оптимальное значение постоянной времени Т_opt @ 0.8 t_и. Получаемое при этом отношение сигнал/шум составляет примерно 0.9q. 

2.4. Нормированные пространства

Рассмотренные выше способы задания метрики обобщают понятие расстояния между двумя точками на плоскости или в пространстве на множества произвольной природы, превращая их в метрические пространства. Аналогично, обобщением понятия длины вектора является норма.

Нормой элемента  произвольного векторного пространства Х, обозначаемой как ||||, называют неотрицательное вещественное число, причем способ отображения Х в множество R₊ (множество неотрицательных вещественных чисел) должен удовлетворять следующим условиям:

1.  |||| = 0, только если  = ;

2.  ||a|| = |a| × |||| , где a – скаляр;

3.  || +|| £ |||| + |||| (неравенство треугольника).

Векторное пространство Х, в котором введена норма, называется нормированным пространством. Норма позволяет ввести в Х метрику, определив расстояние между векторами ,  Î Х как r(, ) = || –||.

Приведем некоторые примеры нормированных пространств.

1.  Если на множестве вещественных чисел R определить ||x|| = |x|, то R становится нормированным пространством.