Сходимость по метрике. Полнота метрических пространств. Принцип сжимающих отображений и его применение. Нормированные пространства, страница 5

1.  Для любых ,  Î L однозначно определен  элемент  Î L, называемый суммой элементов  и , т. е. =+. При этом по отношению к введенной операции сложения векторов L образует абелеву группу. Напомним, что это означает выполнение следующих условий:

·  + ( +) = (+) + (ассоциативность);

·  в L существует нулевой вектор  такой, что для "Î L выполняется равенство  +  =;

·  для "Î Lсуществует элемент  –, называемый обратным для  , такой, что +(–) = ;

·  ",  Î L выполняется равенство + =  +  (коммутативность).

2.  Для " a Î Fи Î L определен элемент aÎ L(произведение вектора на скаляр), причем:

·  a(b) = (ab);

·  е = , где е – нейтральный элемент по отношению к операции умножения в поле F (е = 1 для поля комплексных и вещественных чисел);

·  для " a, b Î F выполняется равенство (a + b) = a + b;

·  ",  Î L и a Î F  a(+) = a + a.

Примеры линейных пространств.

1.  Совокупность действительных чисел с обычными арифметическими операциями сложения и умножения образует ЛП R₁.

2.  Совокупность векторов  = (х₁, х₂, …, х_п), где х_i Î R или С, называют п-мерным линейным арифметическим пространством R_п  или С_п соответственно, если выполняются следующие правила суммирования векторов и умножения на скаляр:  +  = (х₁ + y₁, х₂ + y₂, …, х_п + y_n) и
a = (aх₁, aх₂, …, aх_п).

3.  Непрерывные на отрезке [a, b]  вещественные или комплексные функции с обычными правилами сложения функций и умножения на скаляр образуют ЛП С [a, b].

4.  Аналогично определяется ЛП, элементами которого являются функции с интегрируемым квадратом  L₂[a, b] или L₂.

Линейная зависимость.

Рассмотрим совокупность ненулевых векторов ₁, ₂, …, _n Î L и совокупность  отличных от нуля скаляров a₁, a₂, …, a_п Î F. Вектор 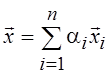 называется линейной комбинацией векторов ₁, ₂, …, _n. Если a_i принимают всевозможные значения из F, то совокупность векторов  образует линейную оболочку системы векторов ₁, ₂, …, _n, которая является линейным подпространством в L. Если "Î L можно представить как сумму 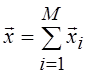, где _i Î L_i, то говорят, что ЛП L представимо в виде прямой суммы линейных подпространств L_i, i = 1, 2, …, M.

Ненулевые вектора ₁, ₂, …, _n называются линейно зависимыми, если существуют не все равные нулю скаляры a₁, a₂, …, a_п такие, что 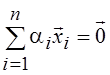. В противном случае вектора называются линейно независимыми. Линейная зависимость означает возможность представить какой-либо вектор системы векторов ₁, ₂, …, _n в виде линейной комбинации остальных. Бесконечная система векторов ₁, ₂, …, _n , … пространства L называется линейно независимой, если линейно независима ее любая конечная подсистема.

Если в L существует п линейно независимых векторов ₁, ₂, …, _n, а любые n + 1 векторов линейно зависимы, то число n называют размерностью пространства L , записывая это утверждение в форме dim L = n. Сами вектора ₁, ₂, …, _n образуют базис п-мерного ЛП L. Если п = ¥, то ЛП называется бесконечномерным. Отметим важнейшие свойства базиса.

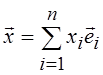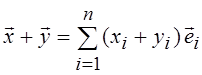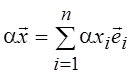1.  Любой вектор  линейного пространства можно записать в виде линейной комбинации базисных векторов , где  – совокупность базисных векторов, а скаляры x_i представляют собой координаты вектора  относительно базиса . Учитывая аксиомы ЛП можно записать  и . Таким образом, базис позволяет свести операции над векторами (сложными объектами) к операциям над скалярами (простыми объектами).

2.  Линейной оболочкой базисной системы векторов является само ЛП L.

Приведем примеры базисных систем. В R_n базисной системой является совокупность п векторов вида  = (1, 0, 0, …, 0),  = (0, 1, 0, …, 0), …, =

= (0, 0, …, 0, 1).

В C[a, b] базисную систему образует совокупность степенных функций
{tⁿ}, n = 0, 1, 2, … . Линейная независимость при конечном п доказывается на основании основной теоремы высшей алгебры, утверждающей, что многочлен степени не выше п вида 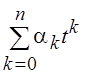 имеет не более п корней, а для линейной зависимости линейная комбинация 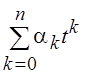 при отличных от нуля коэффициентах должна быть тождественно равна нулю.

На основании теоремы Вейерштрасса любая непрерывная на сегменте [a, b] функция может быть сколь угодно точно аппроксимирована в смысле метрики  многочленом.*