


















Как метрика и норма,
скалярное произведение для ЛП, заданных над полями R или С,
определяется аксиоматически как правило отображения любой упорядоченной пары
<![]() ,
, ![]() >
векторов
>
векторов ![]() и
и ![]() в
множество скаляров из поля R или С, над которыми задано ЛП. Это
правило должно удовлетворять следующим условиям:
в
множество скаляров из поля R или С, над которыми задано ЛП. Это
правило должно удовлетворять следующим условиям:
1.
(![]() ,
, ![]() ) –
неотрицательное вещественное число, равное нулю только, если
) –
неотрицательное вещественное число, равное нулю только, если ![]() =
= ![]() ;
;
2. (![]() ,
, ![]() ) = (
) = (![]() ,
, ![]() )*,
где “*” – знак комплексного сопряжения;
)*,
где “*” – знак комплексного сопряжения;
3.
(a![]() ,
, ![]() ) = a (
) = a (![]() ,
, ![]() );(
);(![]() , a
, a![]() ) = a* (
) = a* (![]() ,
, ![]() ), причем второе равенство является
следствием аксиомы 2 (доказать самостоятельно);
), причем второе равенство является
следствием аксиомы 2 (доказать самостоятельно);
4.
Для ЛП, заданных
над R,скалярное произведение является билинейной
формой (функционалом), по обоим аргументам ![]() и
и ![]() , т. е.
, т. е.
![]() ;
;
![]() ,
,
поскольку для вещественных чисел a* = a.
Опираясь на сформулированные аксиомы, докажем неравенство Коши–Буняковского, играющее очень важную роль в задачах оптимизации. Дело в том, что представив целевую функцию (или ее часть) в виде скалярного произведения, с помощью неравенства (4.1) можно определить ее верхнюю или нижнюю границу, а (4.2) позволяет определить условия достижения этой границы.
Запишем очевидное
неравенство, справедливое для любых векторов ![]() и
и ![]() и значений скаляра l: (
и значений скаляра l: (![]() + l
+ l![]() ,
, ![]() + l
+ l![]() ) ³ 0. Раскрывая его, получим:
) ³ 0. Раскрывая его, получим:
(![]() ,
,![]() ) + l(
) + l(![]() ,
, ![]() ) + l*(
) + l*(![]() ,
, ![]() ) + |l|2 (
) + |l|2 (![]() ,
,![]() ) ³ 0.
) ³ 0.
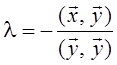 ,
после подстановки и преобразований на основе аксиомы 2, получим:
,
после подстановки и преобразований на основе аксиомы 2, получим:(![]() ,
,![]() ) – 2
) – 2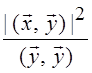 +
+ 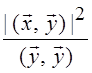 ³ 0,
³ 0,
откуда следует |(![]() ,
, ![]() )|2
£ (
)|2
£ (![]() ,
,![]() )(
)(![]() ,
,![]() ).
).
Приведем классический для
радиотехники пример использования неравенства Коши–Буняковского. Пусть на вход
некоторого фильтра с постоянными параметрами, комплексный коэффициент передачи
которого K(jw) надо определить, подается
стационарный случайный процесс со спектральной плотностью мощности S(w) и сигнал s(t), который полностью известен. Его спектр равен ![]() . Необходимо выбором фильтра, т. е.
подбором K(jw), обеспечить в момент времени t0 максимум отношения сигнал/шум, понимая под ним
. Необходимо выбором фильтра, т. е.
подбором K(jw), обеспечить в момент времени t0 максимум отношения сигнал/шум, понимая под ним
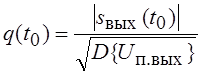 ,
,
где ![]() – дисперсия помехи на выходе фильтра. Будем также предполагать,
что спектральная плотность мощности отлична от нуля на всей частотной оси, т.
е. S(w) > 0.
– дисперсия помехи на выходе фильтра. Будем также предполагать,
что спектральная плотность мощности отлична от нуля на всей частотной оси, т.
е. S(w) > 0.
Пользуясь известными правилами анализа линейных цепей в частотной области [7], можно записать:
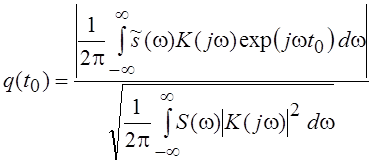 .
.
Представим интеграл, стоящий в
числителе, в виде скалярного произведения двух функций: ![]() и
и
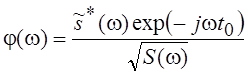 . Использование записи
. Использование записи ![]() является корректным, поскольку
является корректным, поскольку ![]() . Нетрудно заметить, что
. Нетрудно заметить, что 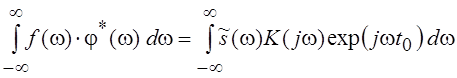 . Применяя неравенство Коши–Буняковского,
получим
. Применяя неравенство Коши–Буняковского,
получим
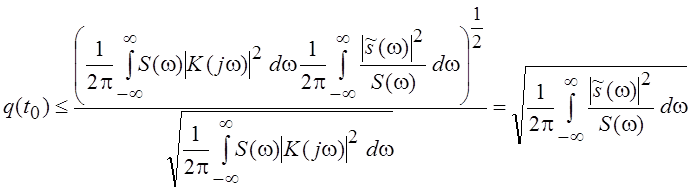 .
.
Максимально достижимое значение q(t0) получим при ![]() ,
где с – скаляр. Таким образом,
,
где с – скаляр. Таким образом,
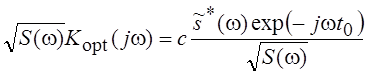 или
или 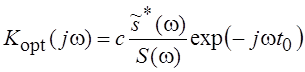 .
.
Константу с, обеспечивающую
отсутствие размерности (K(jw) – безразмерный коэффициент, а
размерность ![]() и S(w) есть В/Гц и В2/Гц соответственно) и не влияющую на величину q(t0), выбирают равной единице.
и S(w) есть В/Гц и В2/Гц соответственно) и не влияющую на величину q(t0), выбирают равной единице.
Если 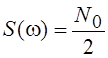 (помеху с такой спектральной плотностью
мощности называют белым шумом), то
(помеху с такой спектральной плотностью
мощности называют белым шумом), то
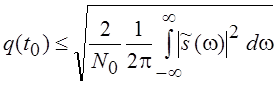 .
.
Как будет показано в гл.5,
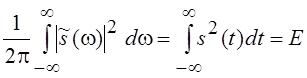 ,
,
где Е – энергия сигнала s(t). Таким образом, максимально достижимое отношение сигнал/шум для сигнала s(t) и помехи типа белый шум определяется выражением
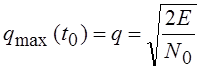 .
.
Частотная
характеристика фильтра, реализующего данный максимум и называемого
согласованным, имеет вид ![]() .
.
В евклидовых пространствах норму и метрику согласовывают с введенным скалярным произведением, полагая
||![]() ||2 = (
||2 = (![]() ,
,![]() ); r(
); r(![]() ,
, ![]() ) = (
) = (![]() –
–![]() ,
, ![]() –
–![]() ).
).
После этого полученное нами неравенство Коши–Буняковского примет окончательный вид (4.1) с условием (4.2).
Два вектора ![]() и
и ![]() называются
ортогональными,
называются
ортогональными, ![]() ^
^![]() , если (
, если (![]() ,
, ![]() ) = 0. Ненулевая совокупность векторов
) = 0. Ненулевая совокупность векторов ![]() называется ортогональной системой, если
для любой пары векторов этой системы скалярное произведение равно нулю, т. е.
называется ортогональной системой, если
для любой пары векторов этой системы скалярное произведение равно нулю, т. е. ![]() при l ¹ m. Если квадрат нормы
каждого вектора ортогональной системы равен единице, то система называется
ортонормальной. Ортогональная система будет в дальнейшем обозначаться как
при l ¹ m. Если квадрат нормы
каждого вектора ортогональной системы равен единице, то система называется
ортонормальной. Ортогональная система будет в дальнейшем обозначаться как ![]() . Для ортогональной системы векторов
. Для ортогональной системы векторов ![]() справедливо равенство
справедливо равенство 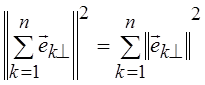 , которое можно рассматривать как обобщение
теоремы Пифагора, считая
, которое можно рассматривать как обобщение
теоремы Пифагора, считая ![]() катетами, а
катетами, а 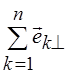 – гипотенузой. Так как ||
– гипотенузой. Так как ||![]() ||2 = (
||2 = (![]() ,
,![]() )
= 0, то с помощью неравенства Коши–Буняковского можно установить следующий
полезный факт. Если (
)
= 0, то с помощью неравенства Коши–Буняковского можно установить следующий
полезный факт. Если (![]() ,
, ![]() ) = 0
при любом ненулевом векторе
) = 0
при любом ненулевом векторе ![]() , то
, то ![]() =
= ![]() .
Доказать это утверждение предоставляется читателю.
.
Доказать это утверждение предоставляется читателю.
Также в качестве упражнения предлагается доказать, что любая ортогональная система ненулевых векторов является линейно независимой.
Скалярное произведение дает
возможность определять координаты вектора ![]() = (х1, х2, …, хп) относительно
произвольного базиса
= (х1, х2, …, хп) относительно
произвольного базиса ![]() , k
= 1, 2, …, п.
, k
= 1, 2, …, п.
Записывая представление
вектора ![]() через базисные вектора,
через базисные вектора, ![]() = =
= =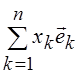 , и
последовательно скалярно умножая обе части этого равенства на базисные вектора
, и
последовательно скалярно умножая обе части этого равенства на базисные вектора ![]() , l = 1, 2,
…, п, получим для определения координат хk
линейную систему уравнений
, l = 1, 2,
…, п, получим для определения координат хk
линейную систему уравнений
(![]() ,
, ![]() ) =
) = 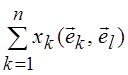 , l = 1, 2,
…, п.
, l = 1, 2,
…, п.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.