Интеграл вероятностей и функции с ним связанные

станты, выбираемые в зависимости от особенности решаемой задачи. В теории вероятностей под интегралом вероятностей понимают функцию 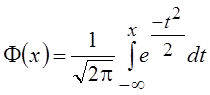, которая является функцией распределения нормальной случайной величины с нулевым средним значением и единичной дисперсией, называемой стандартной нормальной CB N(0, 1).

Функция Φ(x) является дифференцируемой сколь угодное число раз, её производные обозначаются обычно как φ^(k)(x) и образуют ортогональную систему функций. Производная нулевого порядка , а 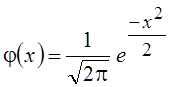  является плотностью вероятности стандартной нормальной СВ N(0, 1). Более подробно об этой ортогональной системе речь пойдёт в разделе, посвящённом полиномам Эрмита. Кроме интеграла вероятностей часто используют интегралы вида 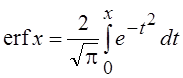 и 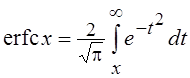, связанные друг с другом соотношением . Каждый из них может быть выражен через Φ(x). Например, .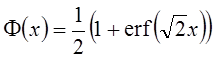

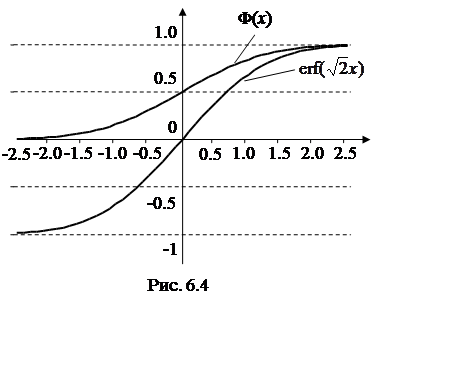
Графики функций Φ(x) и приведены на рис. 6.4.

Из приведённых графиков видно, что табулировать функции Φ(x) и   нужно лишь для x > 0, так как , а . Представление интеграла вероятностей при малых и больших значения аргумента дают соответственно следующие выражения:

 ,

,  .

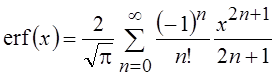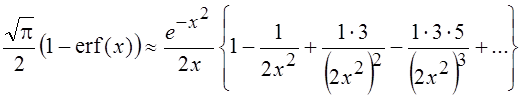Пользуясь связью erf(x) и Φ(x) нетрудно получить аналогичные представления и для Φ(x).

Если комплексная переменная z в (6.12) принимает значения на прямой , то после некоторых преобразований и при соответствующих значениях k, a и b приходим к интегралам Френеля 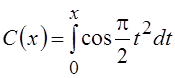 и .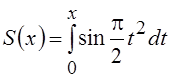

При x = 0  С(0) = S(0) = 0 как интегралы с одинаковыми верхним и нижним пределами. С помощью теоремы о вычетах можно показать (сделать самостоятельно), что .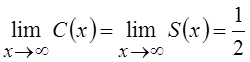

Точки экстремумов интегралов Френеля находятся из уравнений:

 ;   .

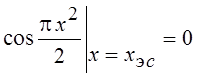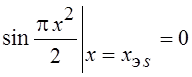Представление при малых значениях аргумента имеет вид

, .

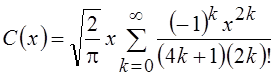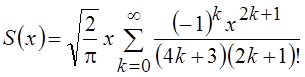Для больших значений аргумента  в качестве первого приближения можно использовать выражения 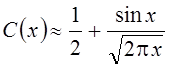 и .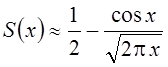

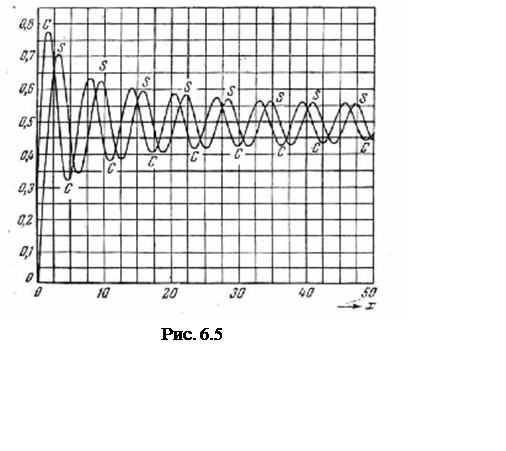
Графики интегралов Френеля приведены на рис. 6.5.

Рассмотрим использование интегралов Френеля в задачах радиотехники на примере отыскания спектра импульса с линейной частотной модуляцией (ЛЧМ-импульса). Такой сигнал был первым, предложенным для устранения противоречия между дальностью действия радиолокационной станции (РЛС) и её разрешающей способностью по дальности, которая существовала при использовании простых сигналов, характеризуемых соотношением , где Δf – ширина спектра, τ_и – длительность импульса.

Дело в том, что при действии помех в виде нормального белого шума дальность действия РЛС определяется энергией сигнала 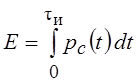, равной при постоянной мощности   и спектральной плотностью мощности нормального белого шума . Если технические возможности повышения p_с и уменьшения  исчерпаны, то для роста E остаётся увеличивать τ_и, что в соответствии с соотношением  ведёт к уменьшению Δf, а это ухудшает разрешающую способность РЛС по дальности, то есть способность раздельно воспринимать две или более близко расположенных цели. Поэтому возникла необходимость в разработке таких сигналов, у которых можно было бы независимо изменять длительность и ширину спектра и, тем самым, получать большие значения произведения , называемого базой сигнала.

Рассмотрим сигнал вида

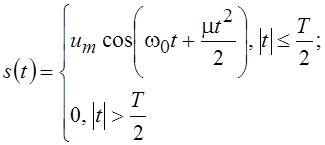
и запишем выражение для его спектра

,

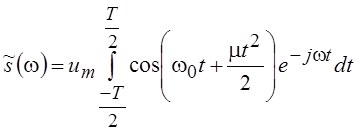где w₀ – центральная частота, μ – крутизна модуляционной характеристики (скорость изменения частоты).

После некоторых преобразований выражение для спектра, соответствующее положительным частотам,  примет вид

  ,

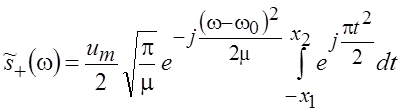где  ,  .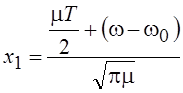 

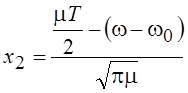Пользуясь формулой Эйлера и определением интегралов Френеля, получим окончательно

.

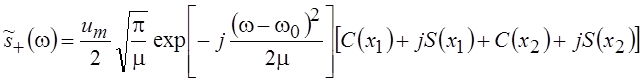Как видно из приведённого выражения, амплитудно-частотный спектр равен

.

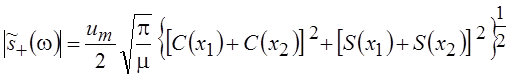Фазовый спектр имеет вид

,

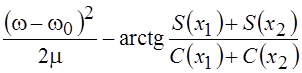причём для случаев интересных для практики вторым слагаемым можно пренебречь. Для нашего сигнала девиация частоты . 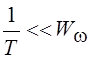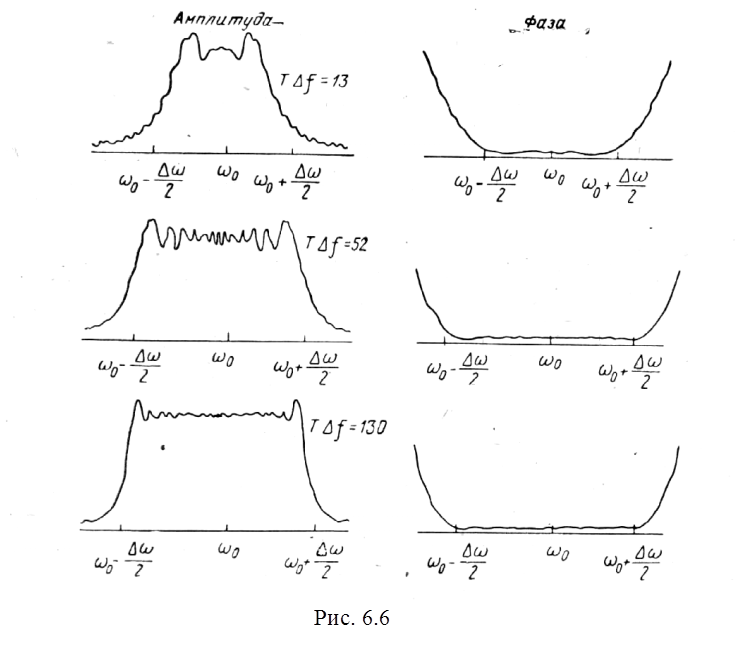Из теории частотной модуляции известно, что, когда девиация частоты во много раз превышает ширину спектра модулирующего колебания (у нас это линейно  нарастающая функция длительностью T и, следовательно, в первом приближении за ширину спектра модулирующего колебания можно принять ), ширина спектра ЛЧМ-импульса близка к W_ω, его база  и он относится к категории сложных сигналов. На рис. 6.6 приведены заимствованные из [13] графики амплитудно-частотных и фазо-частотных спектров ЛЧМ-импульсов при различных значениях базы B.

6.4. Ортогональные многочлены

С ортогональными многочленами мы познакомились в гл.4, рассматривая разные способы построения базисных систем. Там же была отмечена важная роль классических ортогональных многочленов и указан признак, по которому они выделяются из множества ортогональных многочленов.

Прежде, чем более детально заниматься классическими ортогональными многочленами, сформулируем некоторые общие свойства ортогональных полиномов.