Классификация случайных процессов

Глава 4. Классификация случайных процессов

Опираясь на определение СВ, можно дать следующее общее понятие случайного процесса (СП) [1]: Случайным процессом x(t) называется функция двух аргументов j(t, w), где w Î W,  W – множество элементарных событий; t Î T, T – область определения функций  j(t, w). При фиксированном значении t  j(t, w) является случайной величиной, а для каждого фиксированного w (заданного элементарного события) j(t, w) зависит только от t и определяет реализацию СП (траекторию, выборочную функцию). Как и для СВ, область значений j(t, w) может быть счетным (в том числе и конечным) и континуальным множеством Ф.

Классификацию СП можно осуществить по характеру множеств Т и Ф и виду статистической связи между значениями СП, соответствующими различным моментам времени t Î T.

В зависимости от характера множеств Т и Ф случайные процессы можно разделить на четыре класса:

1.  Процессы с дискретными состояниями и дискретным временем (дискретные случайные последовательности);

2.  Процессы с дискретными состояниями и непрерывным временем (дискретные СП);

3.  Процессы с непрерывными состояниями и дискретным временем (случайные последовательности);

4.  Процессы с непрерывными состояниями и непрерывным временем.

На рис. 19 приведены примеры реализаций указанных процессов.

Для классификации СП по виду статистической связи между значениями СП нам потребуется ввести полное статистическое описание случайного процесса. Говорят, что имеется полное статистическое описание СП x(t), если для любых п и t₁, t₂, …, t_n Î T можно задать функцию распределения

.

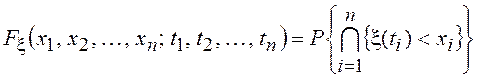При этом должны быть выполнены условие симметрии, состоящее в том, что

,

где  i₁, i₂, …, i_n – перестановка чисел 1, 2, …, п; и условие согласованности:

.

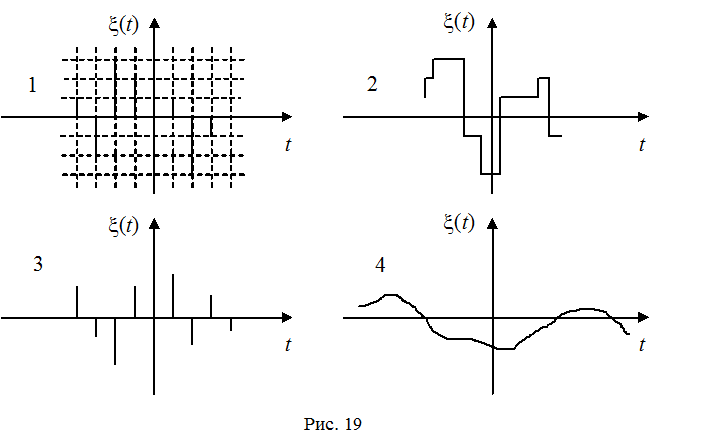
Столь же полное вероятностное описание дадут многомерная ПВ:

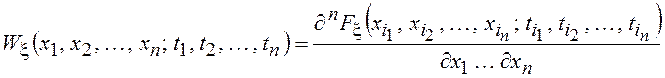
и многомерная ХФ:

,

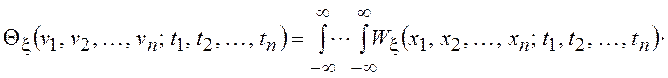
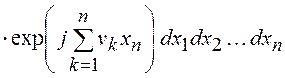или кумулянтная функция:

.

Для дискретных случайных последовательностей (цифровых сигналов), когда множество возможных значений дискретного сигнала конечно или счетно, вероятностное описание дается распределением вида

,

где х₁, х₂, …, х_п – возможные (квантованные) значения процесса (сигнала), а
k₁, k₂, …, k_п – целые числа.

Как и для многомерных случайных величин, для описания случайных процессов могут быть использованы моменты. Начальные и центральные моменты определяются, соответственно, выражениями:

,

.

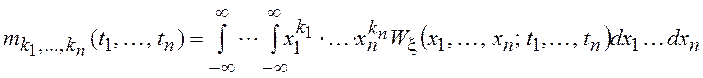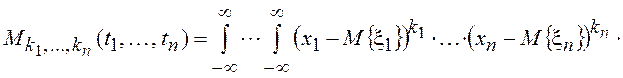
Приведенные выражения зависят от моментов времени t₁, t₂, …, t_n и поэтому называются моментными функциями. Наиболее часто для описания СП используют математическое ожидание (среднее значение) случайного процесса x(t) 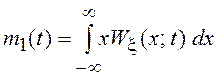 , где t Î T и корреляционную функцию (КФ):

,

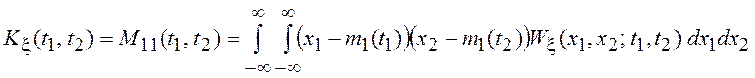где t₁, t₂ Î T . Таким образом, корреляционная функция определяет зависимость ковариации случайных величин x₁ = x(t₁) и x₂ = x(t₂) от моментов времени t₁ и t₂, в которых берутся отсчеты СП x(t). Как и для случайных величин, можно ввести коэффициент корреляции

,

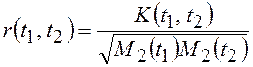где М₂(t₁) и М₂(t₂) – дисперсии отсчетов процесса в моменты времени t₁ и t₂. Напомним, что .

Для того, чтобы функция K(t₁, t₂) была бы корреляционной функцией случайного процесса, она должна быть ядром симметрического положительно определенного интегрального оператора, т. е. K(t₁, t₂) = K(t₂, t₁) и

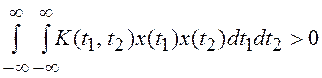
для любых x(t) Î L₂, откуда следует, что K(t, t) > 0.

Если имеется два случайных процесса x(t) и h(t), то можно ввести в рассмотрение взаимную корреляционную функцию:

.

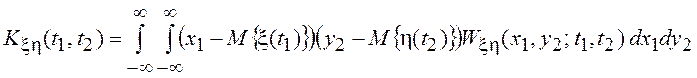Эта функция также положительно определена*, но не симметрична, так как
K_xh(t₁, t₂) = K_hx(t₂, t₁).

Теперь мы подготовлены к тому, чтобы дать классификацию СП по их вероятностным характеристикам.

Наиболее простым с точки зрения вероятностного описания будет СП, у которого любая совокупность значений (отсчетов), взятых в произвольные моменты времени, принадлежащие множеству Т, независима, т. е.

,

, .

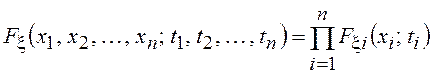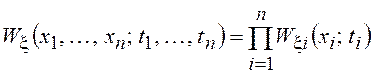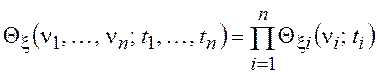Существуют СП, у которых статистические связи распространяются лишь на два соседних отсчета. К их числу относится марковский процесс, для которого

.

Пользуясь представлением многомерной ПВ через условные ПВ, можно по аналогии записать

 ,

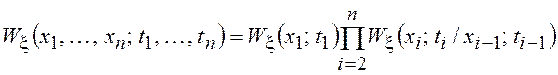а так как 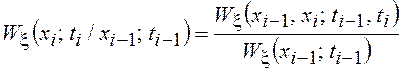 , то ясно, что для марковского процесса многомерная ПВ выражается через двумерные ПВ.

Другим примером СП такого вида является процесс с независимыми приращениями, для которого СВ x₂ – x₁, x₃ – x₂,  …, x_n – x_n-1  независимы для любых п и t₁, t₂, …, t_n Î T. Напомним, что x_i – значение СП в момент t_i. Для того, чтобы записать ПВ любого порядка для процесса с независимыми приращениями, достаточно знать лишь одномерные ПВ x(t) и x(t_i-1) – x(t_i), а так как ПВ разности двух СВ выражается через их совместную ПВ, то для полного вероятностного описания СП с независимыми приращениями достаточно знания двумерной ПВ.

Стационарные СП.

Случайный процесс x(t) называется строго стационарным (стационарным в узком смысле), если его ФР, ПВ или ХФ при любых t, п и t₁, t₂, …, t_n Î T  инвариантны к сдвигу моментов t₁, t₂, …, t_n  на величину t, т. е.

.

Аналогичные выражения можно записать для ФР и ХФ.

СП называется стационарным в широком смысле (по Хинчину), если выполняются более скромные требования:

1.  Среднее значение процесса m₁(t) не зависит от времени, т. е. m₁(t) =

= const;

2.  КФ K_x(t₁, t₂) зависит лишь от разности t₁– t₂ = t, т. е. K_x(t₁, t₂) =
= K_x(t₁– t₂) = K_x(t).

Из второго условия следует, что дисперсия стационарного процесса
D_x(t) = K_x(t, t) = K_x(0) = const.

В силу симметрии K_x(t₁, t₂) корреляционная функция стационарного СП является четной функцией: K_x(–t) = K_x(t).