ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ И ФУНКЦИОНАЛЫ
Оператором называют
отображение элементов одного метрического пространства Х в элементы
другого метрического пространства Y, что кратко
записывается в форме y = Ax. Множество
элементов, на котором определен оператор, называют областью определения ![]() , а соответствующее множество
элементов
, а соответствующее множество
элементов ![]() в Y –
областью значений. Если Y – числовое множество,
то оператор превращается в функционал. Если X – также числовое множество, то речь идет о функции y = f(x). Если уравнение y = Ax разрешимо относительно х
при любом у из области значений оператора А, т. е. х = А–1у, то говорят,
что оператор А обратим, и А–1 – его обратный оператор.
в Y –
областью значений. Если Y – числовое множество,
то оператор превращается в функционал. Если X – также числовое множество, то речь идет о функции y = f(x). Если уравнение y = Ax разрешимо относительно х
при любом у из области значений оператора А, т. е. х = А–1у, то говорят,
что оператор А обратим, и А–1 – его обратный оператор.
Оператор А
непрерывен, если для любой сходящейся последовательности векторов из области
определения 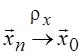 следует
следует 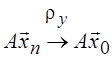 , где rх и rу – метрики ЛП Х
и Y соответственно.
, где rх и rу – метрики ЛП Х
и Y соответственно.
Оператор А
называется ограниченным, если существует такая постоянная С, что для
всякого ![]() выполняется неравенство
выполняется неравенство ![]() . Наименьшее из чисел С называется
нормой оператора и обозначается
. Наименьшее из чисел С называется
нормой оператора и обозначается ![]() . Для любого ограниченного
оператора А, действующего из нормированного пространства в
нормированное, норму
. Для любого ограниченного
оператора А, действующего из нормированного пространства в
нормированное, норму ![]() можно определить следующим образом:
можно определить следующим образом:
![]() =
=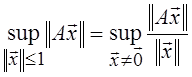 .
.
Понятие оператора широко используется в современной теории систем, описывая связь между входом и выходом системы. В информационных системах последовательное действие операторов (произведение) описывает преобразования, осуществляемые над входными данными в процессе передачи и извлечения полезной информации.
Среди операторов, действующих в линейных нормированных пространствах, наиболее общие результаты можно получить, рассматривая линейные операторы.
Определение.
Пусть Х и Y – линейные нормированные
пространства. Оператор А, действующий из Х в Y
(![]() ), называется линейным, если выполняется
условие, называемое принципом суперпозиции. Для любых
), называется линейным, если выполняется
условие, называемое принципом суперпозиции. Для любых ![]() и
и
![]() , где
, где ![]() – область определения оператора А, а
F – поле, над которым задано ЛП Х, справедливо
равенство:
– область определения оператора А, а
F – поле, над которым задано ЛП Х, справедливо
равенство:
![]() .
.
Это
означает, что линейный оператор аддитивен, ![]() , и
однороден,
, и
однороден, ![]() .
.
Приведем примеры линейных операторов.
1.
Линейный оператор в конечномерных пространствах Rn и Сп. Рассмотрим для определенности Rn с базисом ![]() , k
= 1, 2, …, n. Для произвольного
вектора
, k
= 1, 2, …, n. Для произвольного
вектора ![]() из Rn можно записать
из Rn можно записать 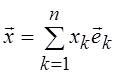 , и в силу линейности
оператора А:
, и в силу линейности
оператора А: 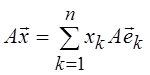 . Таким образом, линейный оператор
полностью определен, если известно, как он действует на базисные вектора.
. Таким образом, линейный оператор
полностью определен, если известно, как он действует на базисные вектора.
Рассмотрим
ЛП ![]() – область значений оператора А и
выберем в нем базис
– область значений оператора А и
выберем в нем базис ![]() , l = 1, 2, …, m, m £ n. Тогда можно записать
, l = 1, 2, …, m, m £ n. Тогда можно записать 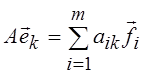 , где aik – координаты
преобразованного базисного вектора
, где aik – координаты
преобразованного базисного вектора ![]() относительно базиса
относительно базиса ![]() , и
, и 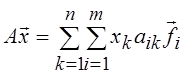 .
.
Таким
образом, результат действия любого линейного оператора А на
вектор ![]() в конечномерном пространстве сводится к
умножению вектора
в конечномерном пространстве сводится к
умножению вектора ![]() на матрицу оператора
на матрицу оператора ![]() , i = 1, 2, …, m; k = 1, 2, …, n. Ранг этой
матрицы (наивысший порядок отличных от нуля миноров) определяет размерность
подпространства
, i = 1, 2, …, m; k = 1, 2, …, n. Ранг этой
матрицы (наивысший порядок отличных от нуля миноров) определяет размерность
подпространства ![]() (область значений оператора А).
Если
(область значений оператора А).
Если ![]() = Х и
= Х и ![]() =Y (оператор А отображает Х на Х), то
базисные системы
=Y (оператор А отображает Х на Х), то
базисные системы ![]() и
и ![]() совпадают
и координаты aik (элементы
матрицы оператора) вычисляются относительно исходного базиса
совпадают
и координаты aik (элементы
матрицы оператора) вычисляются относительно исходного базиса ![]() .
.
2. Рассмотрим оператор поворота вектора на плоскости на
угол j. Ортонормальным базисом в R2 будет система векторов
![]() = (1, 0),
= (1, 0), ![]() = (0,
1). Преобразованные (повернутые на угол j)
базисные вектора можно записать в исходном базисе как
= (0,
1). Преобразованные (повернутые на угол j)
базисные вектора можно записать в исходном базисе как ![]() и
и
![]() . Таким образом, матрица поворота любого
вектора на плоскости имеет вид
. Таким образом, матрица поворота любого
вектора на плоскости имеет вид
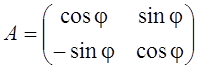 .
.
Вектор ![]() = (–3, 2) после поворота на угол j будет иметь вид
= (–3, 2) после поворота на угол j будет иметь вид
А![]() = (–3cos
j – 2sin j, –3sin j + 2 cos j).
= (–3cos
j – 2sin j, –3sin j + 2 cos j).
3.
Важную роль играет тождественный, или единичный, оператор Е,
который любой вектор из Х превращает в самого себя, т. е. E![]() =
=![]() . Для Rn этот оператор
определяется единичной матрицей Е.
. Для Rn этот оператор
определяется единичной матрицей Е.
3.
Рассмотрим наиболее употребительные линейные операторы в функциональных
пространствах C [a, b]
и L2 [a,
b]. Простейшим оператором в C [a, b] и L2 [a, b] является умножение произвольной функции
f(t) Î C [a, b] или L2 [a, b] на фиксированную функцию ![]() , также принадлежащую рассматриваемым ЛП,
т. е. А f(t) =
, также принадлежащую рассматриваемым ЛП,
т. е. А f(t) = ![]() f(t).
f(t).
Весьма важным является
оператор дифференцирования![]() . Областью его
определения в С [a, b] и L2 [a, b]
является множество дифференцируемых функций. Более общим является
дифференциальный оператор n-го порядка Dn, определяемый как
. Областью его
определения в С [a, b] и L2 [a, b]
является множество дифференцируемых функций. Более общим является
дифференциальный оператор n-го порядка Dn, определяемый как 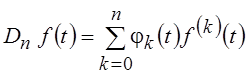 , где jk(t) – фиксированные
функции. Областью определения оператора Dn является множество n раз
дифференцируемых функций.
, где jk(t) – фиксированные
функции. Областью определения оператора Dn является множество n раз
дифференцируемых функций.
Так, например, оператор 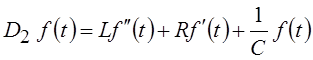 определяет собственные колебания тока f(t)
= i(t) в последовательном колебательном контуре.
определяет собственные колебания тока f(t)
= i(t) в последовательном колебательном контуре.
Большую роль в приложениях
играют интегральные операторы Фредгольма 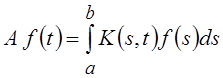 и
Вольтерра
и
Вольтерра 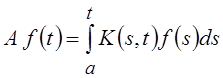 . Здесь функция двух переменных K(s,
t) называется ядром оператора. Обычно для
. Здесь функция двух переменных K(s,
t) называется ядром оператора. Обычно для
С [a, b] предполагается непрерывность K(s, t)
по обоим аргументам, а для
L2 [a, b] – интегрируемость квадрата ядра, т.
е. 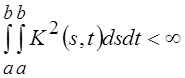 . Для оператора Вольтерра обычно
предполагается, что функция K(s, t) непрерывна при s
< t и K(s, t) = 0 при s > t.
. Для оператора Вольтерра обычно
предполагается, что функция K(s, t) непрерывна при s
< t и K(s, t) = 0 при s > t.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.