Линейные операторы и функционалы. Часть 1, страница 4

Таким образом, если для исходного оператора интегрирование ядра ведется по первой переменной, то для сопряженного оператора – по второй. Для комплексного Н 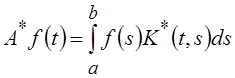, где символ "*" над К(t, s) означает комплексное сопряжение.

Оператор А называется самосопряженным, если А^* = А, что означает выполнение равенства .

Для линейного оператора в R_n это означает самосопряженность матрицы А, т. е. А – симметрическая матрица. Для С_n оператор А – эрмитова матрица.

Для рассмотренного выше оператора Фредгольма самосопряженность означает симметричность ядра оператора по обеим переменным, т.  е. выполнение равенств К(s, t) = К(t, s) для вещественного Н и К(s, t) = К^*(t, s) для комплексного.

В операторах Фредгольма и Вольтерра часто приходится сталкиваться с ядрами, зависящими от разности переменных s – t, т. е. К(s, t) = К(s – t). Такие ядра называют ядрами разностного типа. Для самосопряженных операторов К(s – t) = К(t – s), т. е. К является четной функцией переменных t = s – t. Позже мы столкнемся с такими ядрами при изучении стационарных случайных процессов. С ядрами разностного типа мы также встречаемся при изучении отклика линейной стационарной системы (системы с постоянными параметрами) на входное воздействие.

Давая определение линейного функционала , мы подчеркивали, что  – фиксированный вектор. Если  связан с вектором , то функционал  перестает быть линейным. Для дальнейшего чрезвычайно важен функционал вида , называемый квадратичной формой. В R_n  или C_n квадратичная форма определяется матрицей А. Для квадратной матрицы (А действует из R_n  в R_n) 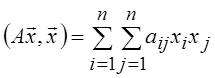; для C_n .

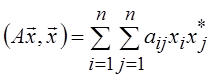В L₂[a, b] квадратичная форма может быть определена для оператора Фредгольма как 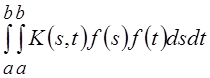, для комплексного варианта L₂[a, b] вместо f(t) берется комплексно сопряженная функция  f ^*(t).

Вещественная квадратичная форма называется положительно (неотрицательно) определенной, если соответственно  > 0 или  ³ 0 для всех ненулевых векторов  из области определения оператора А.

Для квадратичной формы, заданной в R_n, матрица А, определяющая положительно определенную квадратичную форму, удовлетворяет следующим требованиям:

–  все главные миноры являются положительными;

–  все коэффициенты характеристического многочлена отличны от нуля и имеют чередующиеся знаки;

–  все собственные значения имеют положительные вещественные части.

Если А – самосопряженный оператор, то соответствующая ему квадратичная форма вещественна.

Для самосопряженных операторов справедливо следующее важное утверждение.

Собственные значения самосопряженного оператора вещественны и соответствующие им собственные вектора ортогональны. Вспомним разговор о способах построения ортогональных систем. Ввиду важности этого утверждения и его приложений докажем эту теорему для вещественных Н пространств.

Пусть l – собственное значение оператора А, а  – соответствующий ему собственный вектор, т. е. . Умножим скалярно обе части этого равенства на . Тогда . Левая часть в силу самосопряженности А вещественна, поскольку ;  – вещественен и положителен. Следовательно, l – вещественное число. Для положительно определенных самосопряженных операторов  > 0 для " и l – вещественно и положительно.

Пусть l_i  и l_j – два различных собственных значения, а  и  соответствующие им собственные вектора, т. е.   и . Умножая скалярно обе части первого уравнения на , а второго на  и почленно вычитая, получим . Пользуясь тем, что А – самосопряженный оператор и для вещественных пространств скалярное произведение коммутативно, т. е. , можно утверждать, что левая часть записанного выражения равна нулю и в силу различия собственных значений .