В Rn любой линейный функционал имеет вид  , где
, где
![]() = (х1, х2,
…, хп) – аргумент функционала,
= (х1, х2,
…, хп) – аргумент функционала, ![]() = (а1, а2,
…, ап) – фиксированный вектор из Rn. Линейность данного функционала
вытекает из аксиом ЛП.
= (а1, а2,
…, ап) – фиксированный вектор из Rn. Линейность данного функционала
вытекает из аксиом ЛП.
В С [a, b]
примером линейного функционала может служить интеграл вида 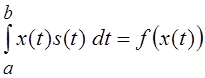 , называемый в задачах обработки сигналов
корреляционным интегралом, где x(t) является аргументом, а s(t)
– фиксированной функцией, т.е., как уже отмечалось, скалярное произведение при
фиксированном втором сомножителе по отношению к первому является линейным
функционалом.
, называемый в задачах обработки сигналов
корреляционным интегралом, где x(t) является аргументом, а s(t)
– фиксированной функцией, т.е., как уже отмечалось, скалярное произведение при
фиксированном втором сомножителе по отношению к первому является линейным
функционалом.
Очень важным является
линейный функционал, для которого ![]() , где
, где ![]() – функция, равная нулю всюду, кроме точки t
= t0,
– функция, равная нулю всюду, кроме точки t
= t0,
t Î(a, b),
и принимающая в t0 бесконечно
большое значение. При этом 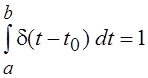 . Функция
. Функция ![]() называется дельта-функцией Дирака и более
подробно будет рассмотрена ниже.
называется дельта-функцией Дирака и более
подробно будет рассмотрена ниже.
Рассмотрим геометрический
смысл линейного функционала. Выберем для наглядности в качестве ЛП R3 – трехмерное арифметическое пространство. Линейный
функционал 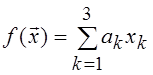 в R3 задает плоскость, определяемую уравнением
в R3 задает плоскость, определяемую уравнением 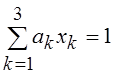 , где
, где ![]() = (а1, а2,
а3) – фиксированный вектор. Каждому
вектору
= (а1, а2,
а3) – фиксированный вектор. Каждому
вектору ![]() соответствует точка на этой плоскости. Для
произвольного ЛП линейный функционал задает гиперплоскость.
соответствует точка на этой плоскости. Для
произвольного ЛП линейный функционал задает гиперплоскость.
Выпуклые множества и выпуклые функционалы.
Понятие выпуклости лежит в основе многих разделов теории ЛП. Оно является ключевым при решении многих задач оптимизации (выпуклое программирование)*.
Пусть L –
некоторое ЛП. Подпространство M Ì L называется выпуклым, если для ![]() все вектора вида
все вектора вида ![]() ,
где
,
где ![]() , также принадлежат М.
Геометрический смысл этого определения ясен из рис. 5.1, на котором приведены
выпуклое а) и невыпуклое б) подпространства в R2 (на плоскости).
, также принадлежат М.
Геометрический смысл этого определения ясен из рис. 5.1, на котором приведены
выпуклое а) и невыпуклое б) подпространства в R2 (на плоскости).

Для С [a, b] множество функций, удовлетворяющих условию | f(t)| £ 1, выпукло, так как если | f(t)| £ 1 и | g(t)| £ 1, то
![]() .
.
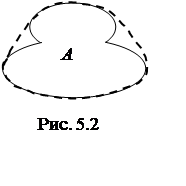
Для произвольного множества A Ì L существует наименьшее выпуклое множество, которое содержит А. Оно называется выпуклой оболочкой множества А. На рис. 5.2 пунктиром показана оболочка множества А.
 Важным примером выпуклой оболочки
является
Важным примером выпуклой оболочки
является
п-мерный симплекс, который определяется следующим образом. Симплекс с
вершинами ![]() 1,
1,
![]() 2,
…,
2,
…, ![]() п + 1 есть совокупность всех точек, представимых в виде
п + 1 есть совокупность всех точек, представимых в виде
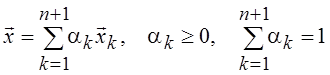 .
.
При этом вектора ![]() 2
–
2
– ![]() 1,
1,
![]() 3
–
3
– ![]() 1,
…,
1,
…, ![]() п + 1
–
п + 1
– ![]() 1
должны быть линейно независимы. В Rn нуль-мерный симплекс – это точка, одномерный –
отрезок, двумерный – треугольник, трехмерный – тетраэдр.
1
должны быть линейно независимы. В Rn нуль-мерный симплекс – это точка, одномерный –
отрезок, двумерный – треугольник, трехмерный – тетраэдр.
С понятием выпуклости множества тесно связано понятие выпуклого функционала.
Определение.
Неотрицательный
функционал p(![]() ) ³ 0 для "
) ³ 0 для " ![]() Î L называется выпуклым, если выполняются
следующие условия:
Î L называется выпуклым, если выполняются
следующие условия:
1. ![]() для "
для " ![]() ,
, ![]() Î L;
Î L;
2. p(a![]() ) = ap(
) = ap(![]() ) для всех a > 0.
) для всех a > 0.
Примером выпуклого функционала может служить норма, так как сформулированные условия включаются в систему аксиом, определяющих норму.
Напомним, что гильбертовым называется бесконечномерное полное евклидово пространство H. В зависимости от того, над каким полем построено исходное ЛП (R или С) различают вещественное и комплексное H-пространства.
Для линейных функционалов ![]() в Н ключевой является теорема, утверждающая,
что любой линейный функционал в Н имеет вид
в Н ключевой является теорема, утверждающая,
что любой линейный функционал в Н имеет вид ![]() , где вектор
, где вектор ![]() однозначно
определяет функционал
однозначно
определяет функционал ![]() . При этом
. При этом ![]() .
.
Для линейных функционалов 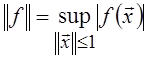 . Опираясь на неравенство Коши–Буняковского
и сформулированную выше теорему, можно доказать предыдущее утверждение.
. Опираясь на неравенство Коши–Буняковского
и сформулированную выше теорему, можно доказать предыдущее утверждение.
Пусть А – линейный
оператор в гильбертовом пространстве Н. Рассмотрим функционал ![]() , где
, где ![]() –
фиксированный вектор из Н. Очевидно, что
–
фиксированный вектор из Н. Очевидно, что ![]() –
линейный функционал и в соответствии со сформулированной выше теоремой
–
линейный функционал и в соответствии со сформулированной выше теоремой ![]() . Выражая
. Выражая ![]() через
через ![]() с помощью оператора А*
получим окончательно
с помощью оператора А*
получим окончательно ![]() . Оператор А*
называется сопряженным к А. Его норма
. Оператор А*
называется сопряженным к А. Его норма ![]() равна
норме исходного оператора, т. е.
равна
норме исходного оператора, т. е. 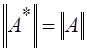 .
.
Понятие сопряженного
оператора может быть введено в любом евклидовом пространстве. Так в Rn,где любой линейный
оператор определяется матрицей А, сопряженным будет оператор,
задаваемый сопряженной матрицей А*. Напомним, что
элементы сопряженной матрицы ![]() равны элементам aji исходной матрицы.
В вещественном гильбертовом пространстве L2[a, b] для интегрального оператора
Фредгольма
равны элементам aji исходной матрицы.
В вещественном гильбертовом пространстве L2[a, b] для интегрального оператора
Фредгольма 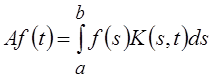 сопряженным будет оператор
сопряженным будет оператор 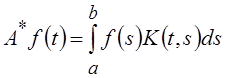 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.