Линейные операторы и функционалы. Часть 1, страница 5

Для любого самосопряженного линейного оператора в Н справедлива фундаментальная теорема Гильберта–Шмидта, утверждающая, что для названного оператора А существует ортонормальная система  собственных векторов, отвечающих собственным значениям {l_k}, такая, что  представляется единственным образом в виде 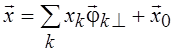, где х_k – координаты (коэффициенты Фурье) вектора  относительно системы , а  – удовлетворяет условию . При этом 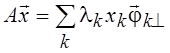. Если система  бесконечна, то l_k ® 0 при k ® ¥.

Сформулированная теорема означает, что для всякого самосопряженного оператора А в подпространстве Н существует ортогональный базис, состоящий из собственных векторов этого оператора. Еще раз вспомним наш разговор о способах построения ортогональных систем.

Вообще говоря, данная теорема справедлива для самосопряженных и компактных операторов, но для подавляющего большинства встречающихся в радиотехнике операторов условия компактности оператора выполняются.

Часто теорема Гильберта–Шмидта формулируется для вполне непрерывных самосопряженных операторов. Линейный оператор А называется вполне непрерывным, если он может быть с любой точность аппроксимирован конечномерным оператором, т. е. может быть представлен в виде суммы конечномерного оператора и оператора со сколь угодно малой нормой.

При решении многих задач математической физики, а также в иных приложениях чрезвычайно продуктивными являются самосопряженные дифференциальные операторы и соответствующие им самосопряженные дифференциальные уравнения. Рассмотрим этот вопрос на примере определенного на промежутке [a, b] дифференциального оператора второго порядка . Функции j_i(t), i = 0, 1, 2 вещественны и имеют в области a £ t £ b непрерывные производные i-го порядка. Кроме того, функция j₂(t) не должна иметь нулей при t Î(a, b).

Оператор , самосопряженный с D₂, определяется следующим образом:

.

Сопоставление выражений для  и  определяет необходимое и достаточное условие самосопряженности оператора D₂: . При выполнении этого условия оператор D₂ принимает вид

 =  ,

где r(t) = j₂(t), a q(t) = j₀(t).

Данный самосопряженный дифференциальный оператор второго порядка называется оператором Штурма–Лиувилля. Его собственные функции, образующие ортогональную систему, широко используются при решении разнообразных радиотехнических задач.

Так, например, если а = –p, b = p, r(t) = –1, q(t) = 0, и краевые условия выбраны следующим образом: f(–p) = f(p), f ¢(–p) = f¢ (p), то = –f²(t),  и собственные значения и собственные функции находятся из уравнения
– f²(t) = lf(t), решением которого будут функции exp(jt), exp(–jt) или их линейные комбинации cost  и  sint. В силу линейной независимости cost  и  sint общее решение будет иметь вид

f(t) = C₁cost  + C₂sint.

С учетом краевых условий получим следующее выражение для собственных значений оператора: l_k = k², k = 0, 1, 2, … . Каждому собственному значению l_k соответствуют две линейно независимые функции cos kt и sin kt, образующие при k = 0, 1, 2, … хорошо знакомую нам ортогональную на промежутке [–p, p] систему {cos kt, sin kt}, разложение по которой дает ряд Фурье.

Рассмотрим вопрос о собственных функциях произвольного дифференциального оператора второго порядка, т. е. о решениях дифференциального уравнения  = lf(t), или, в развернутом виде с заменой l на –l,

.

Умножая левую и правую части на функцию r(t), удовлетворяющую условию , получим:

,

где . Таким образом, уравнение для определения собственных функций оказалось записанным в самосопряженной форме. Собственные функции, отвечающие различным собственным значениям l_k и  l_l, будут теперь ортогональны с весом, т. е. 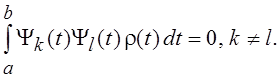 Условие, которому должна удовлетворять функция r(t), можно переписать в виде

,

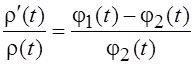в котором мы узнаем дифференциальное уравнение для весовой функции, определяющей для рассматриваемого промежутка систему классических ортогональных многочленов (см. параграф 6.4).