Классификация случайных процессов, страница 2

При экспериментальных исследованиях СП, когда мы имеем дело с одной реализацией, важным является понятие эргодичности случайного процесса. Дело в том, что для стационарных процессов можно ввести операцию временного усреднения на основе одной реализации x(t) случайного процесса x(t). Для обозначения операции временного усреднения часто используют волнистую черту над усредняемым выражением:

.

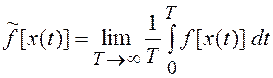Например, для среднего значения, корреляционной функции и дисперсии получим:

, ,

.

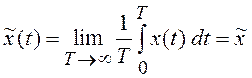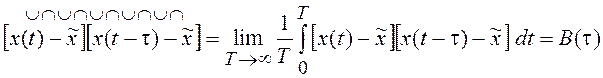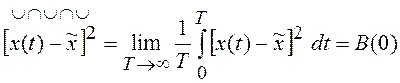Естественно, возникает вопрос, как соотносятся между собой характеристики процесса, полученные путем статистического усреднения (с помощью ПВ), и средние по времени. В  этой связи дадим определение [6]. Стационарный в узком смысле процесс называется эргодическим, если любые его вероятностные характеристики, найденные на основе статистического усреднения, по множеству реализаций, с вероятностью сколь угодно близкой к единице совпадают с соответствующими средними по времени. Иными словами, если известна одна единственная реализация процесса для , то путем сдвигов по времени может быть получен бесконечный статистический ансамбль реализаций. Следовательно, по одной реализации можно узнать возможные вероятностные характеристики [7].

Часто понятие эргодичности связывают с конкретной вероятностной характеристикой, например, со средним значением, называя эргодическим такой СП, для которого . При таком определении СП может быть эргодическим, но нестационарным [8].

Пусть, например, , где h – СВ, у которой Мh = 0, а . В смысле данного определения процесс является эргодическим, поскольку

.

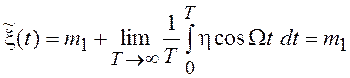Но он не является стационарным в силу зависимости его дисперсии

от времени.

Мы в дальнейшем будем опираться на первое определение.

Эргодичность процесса можно определить на основе условной ПВ . Для стационарного в узком смысле процесса одномерная ПВ W_x(x₀; t) не зависит от времени, а двумерная W_x(x₁, x₂; t₁, t₂) зависит только от разности  t₁– t₂ = t, поэтому условная ПВ

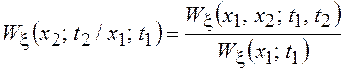
для стационарного процесса будет равна

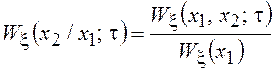
и будет зависеть только от t₁– t₂ = t.

Если  и не зависит от х₁, то процесс x(t) называется эргодическим. Иными словами, требуется, чтобы отсчеты стационарного процесса в любые моменты времени  t₁ и t₂  при t₁– t₂ ®¥ становились бы независимыми. Для нормального случайного процесса, ПВ отсчетов которого задается многомерным нормальным распределением (см. раздел 2), это условие выполняется, если корреляционная функция стремится к нулю, когда  t ®¥, т. е. K_x(t) = 0.

Для эргодического процесса имеет место важное свойство, используемое для экспериментального определения ПВ и ФР. Оно связано с временем пребывания эргодического процесса между двумя уровнями х₁ и х₂ (см. рис. 20).

Предел отношения  при Т ®¥ равен вероятности попадания отсчетов СП в промежуток (х₁,  х₂), т. е. 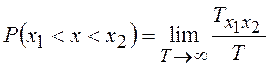. Если
х₁ – х₂ = Dх достаточно мало, то Р(х₁ < x < х₂) = W_x(x) Dx  и

.

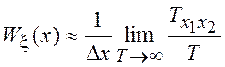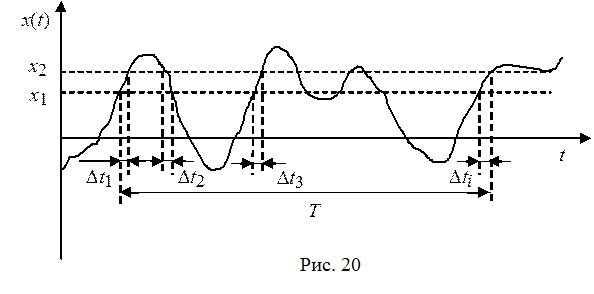
При х₁ = –¥ получаем возможность для оценки ФР, так как  Р(< x < х₂) =
= F(x₂). Важную роль в радиотехнике играют квазидетерминированные процессы. Квазидетерминированный процесс определяется как совокупность функций времени t заданного вида , зависящих от случайного параметра  – случайного вектора. Иногда такие СП называют элементарными случайными функциями.

Например, , где А, w, q – случайные величины с  совместной ПВ W ( А, w, q).

Другим примером квазидетерминированного процесса, часто встречающимся в задачах радиотехники, является сигнал вида

,

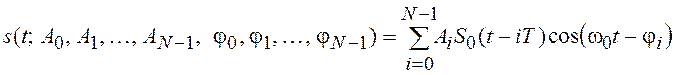представляющий собой группу (пачку) из N радиоимпульсов с несущей частотой w₀, сдвинутых друг относительно друга на величину Т, имеющих детерминированную огибающую S₀(t) и случайные амплитуды A_i, A_i > 0 и фазы j_i, j_i Î [–p, p], определяемые ПВ .

При прохождении сигнала s(t) многолучевого канала на входе приемника наблюдается процесс вида 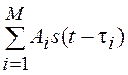, где {A_i; t_i}, i = 1, 2, …, M – совокупность случайных амплитуд A_i, определяемых ослаблением сигнала в соответствующем луче, и случайных задержек  t_i, связанных с запаздывани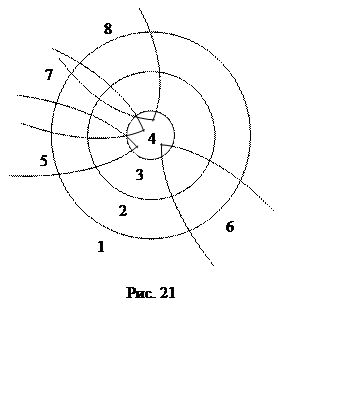ем сигнала при распространении. Рассмотренная классификация может быть образно представлена с помощью “галактики” случайных процессов [8], приведенной на рис. 21. На рис. 21 приняты следующие обозначения: 1 – нестационарные СП; 2 – стационарные в широком смысле СП; 3 – стационарные в узком смысле СП; 4 – эргодические СП; 5 – квазидетерминированные СП; 6 – СП с независимыми значениями; 7 – марковские СП; 8 – СП с независимыми приращениями.

Контрольные вопросы

1. Дайте определение случайной функции, случайного процесса.

2. По каким признакам осуществляется классификация СП?

3. Что дает полное статистическое описание СП?

4. Запишите выражения для математического ожидания  и корреляционной функции  СП.

5. Как определяется взаимная корреляционная функция СП  и ?

6. Дайте определение СП с независимыми отсчетами, марковского СП, СП с независимыми приращениями.

7. Дайте определение СП, стационарного в широком и узком смыслах.

8. Как определяется операция усреднения по времени для стационарного СП?

9. Запишите корреляционную функцию стационарного СП на основе усреднения по времени.

10. Дайте определение эргодического СП.

11. Как для эргодического СП можно получить оценки ПВ и ФР?

12. Что называется квазидетерминированным СП? Приведите примеры.