Корреляционные и спектральные характеристики случайных процессов

Глава 5. Корреляционные и спектральные характеристики

случайных процессов

Для детерминированных сигналов исчерпывающим описанием является задание функции s(t), определяющей поведение сигнала во временной области или преобразования Фурье функции s(t), при условии, что оно существует, 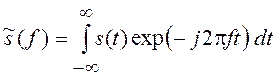, называемое спектром сигнала. Для случайных процессов аналитическое задание каждой реализации как функции времени, за исключением квазидетерминированных СП, невозможно, но некоторое представление о поведении реализации СП во времени можно получить с помощью КФ рассматриваемого процесса. Напомним, что КФ показывает, как меняется корреляционная связь между отсчетами СП, расположенными в моменты времени t₁ и t₂. Если эта связь быстро изменяется, то соответственно быстро будет меняться и КФ. Реализации такого процесса будут быстро меняющимися функциями времени. Для иллюстрации на рис. 22 приведены реализации (слева) и КФ (справа) для двух стационарных СП.

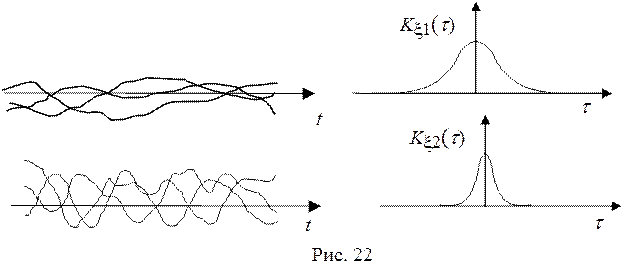
Дисперсии процессов x₁(t) и x₂(t) предполагаются одинаковыми. Преобразование Фурье реализаций СП 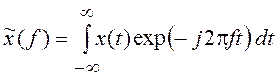, если оно существует, является случайной функцией переменной  f  и, как и сама реализация x(t), не может быть использована для описания СП.

Для стационарного СП в качестве характеристики в частотной области используется преобразование Фурье от КФ

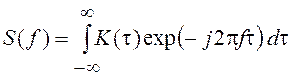,                                 (5.1)

называемое спектральной плотностью СП. Если СП x(t) описывает случайный ток, случайное напряжение или случайную напряженность поля, то S(f) называют спектральной плотностью мощности (СПМ) или энергетическим спектром флуктуаций процесса x(t). Флуктуациями называют отклонение значений процесса x(t) от среднего значения.

Корреляционная функция выражается через спектральную плотность мощности с помощью обратного преобразования Фурье:

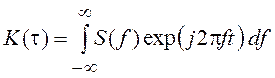,                                 (5.2)

Формулы (5.1) и (5.2) определяют содержание теоремы Винера–Хинчина, утверждающей, что КФ и спектральная плотность связаны друг с другом преобразованием Фурье.

Учитывая, что K(0) = Dx(t) = 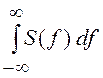, можно утверждать, что спектральная плотность S(f) определяет в общем случае распределение дисперсии СП по частоте. Для случайных напряжения и тока S(f) описывает распределение средней мощности, выделяемой на резисторе с сопротивлением 1 W, по спектру.

Остановимся более подробно на свойствах КФ и спектральной плотности стационарных СП. Прежде всего отметим, что спектральная плотность S(f), как преобразование Фурье четной функции K(t), является вещественной четной функцией. Будучи распределением по спектру неотрицательной характеристики СП – дисперсии,  S(f) ³ 0. Это означает, что КФ должна иметь неотрицательное преобразование Фурье. Кроме того, КФ стационарного СП, как уже отмечалось, должна быть четной функцией t, т. е. K(–t) = K(t). Также справедливо неравенство K(0) = Dx(t) = s² ³ |K(t)|, поскольку

.

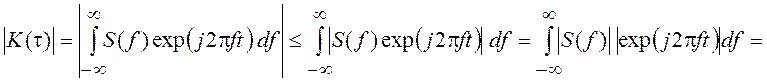
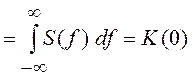Напомним, что так как S(f) ³ 0, то | S(f) | = S(f). Знак равенства в полученном соотношении  £ K(0) достигается для периодических СП, например, для процесса , где U_m и w₀ – детерминированные величины, а q – случайная величина с ПВ

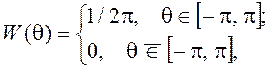
корреляционная функция, как будет показано ниже, равна .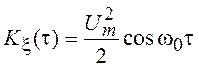

Для непериодических СП K(t) с ростом t  стремится к нулю апериодически или совершая затухающие колебания.

Числовой характеристикой спектральной плотности S(f) является эффективная ширина спектра СП Df_э, определяемая как 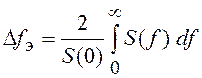 для СП, у которых S(f) группируется около нулевой частоты, т. е. видеопроцессов (см. рис. 23, а), и 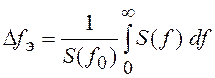 , если S(f) группируется около частот ±f₀, где 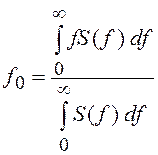   – средняя или центральная частота (см. рис. 23, б). Такие СП называются радиопроцессами.

Зависимость корреляционной функции от t показывает, как меняется статистическая, точнее, корреляционная связь между значениями СП, разделенными интервалом протяженностью t. Интервал, для которого эта связь становится пренебрежимо малой, называют временем корреляции СП и обозначают как t_к. Количественное определение t_к может быть различным и зависит от вида корреляционной функции и решаемых задач. Для неотрицательных корреляционных функций t_к определяют как 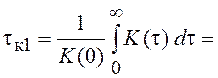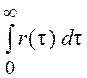, если 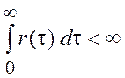. Более общим, включающим и приведенное определение, будет представление t_к в виде .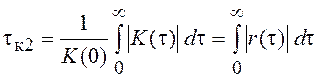

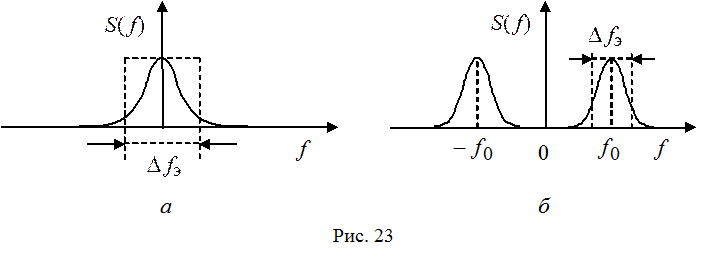
Можно определить t_к3 как такое значение t, начиная с которого будет выполняться неравенство |r(t)| < a, где 0 < a < 1. Обычно задаются значением
a = 0,05.

Для СП имеет место соотношение неопределенности, заключающееся в том, что произведение ширины спектра и времени корреляции равно константе, величина которой зависит от определения Df и t_к. Так, для

,

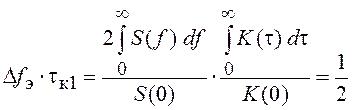поскольку 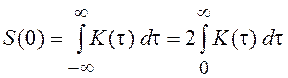 и .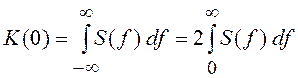

Рассмотрим наиболее часто встречающиеся спектральные плотности S(f) и соответствующие им КФ K(t).

1.  “Белый” шум.

Для “белого” шума S(f) =  и K(t) =d(t). Как процесс, имеющий дисперсию (среднюю мощность), равную бесконечности, он является математической абстракцией, удобной для проведения расчетов. Реальный СП заменяют “белым” шумом при анализе прохождения СП через линейную систему при условии, что спектральная плотность СП постоянна в полосе пропускания системы (см. рис. 24, а).

Финитный “белый” шум.

Этот процесс имеет спектральную плотность вида 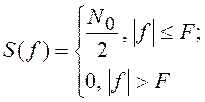 и 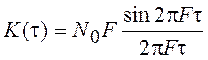 (рис. 24, б). Дисперсия процесса равна K(0) = N₀F.

3. “Полосовой” шум с прямоугольным энергетическим спектром.

СПМ данного процесса имеет вид

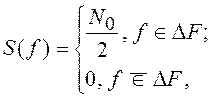
где 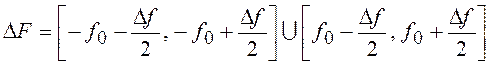, а корреляционная функция равна 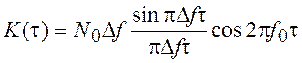 (рис. 24, в). Дисперсия процесса, как и в предыдущем примере, равна K(0) = N₀Df.

4.  Видеопроцесс с гауссовским энергетическим спектром.

Для такого процесса

;  .

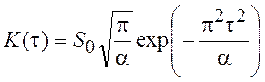Дисперсия процесса 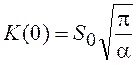. Параметр a определяет ширину энергетического спектра 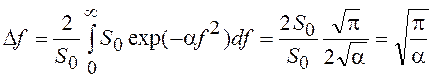 (рис. 24, г).

5.  “Полосовой” шум с гауссовским  энергетическим спектром.