Корреляционные и спектральные характеристики случайных процессов, страница 4

Так как состояния U_m и –U_m равновероятны, что вытекает из стационарности процесса, то выполняются равенства

;  .

Среднее значение и дисперсия процесса x(t)  будут равны

;

.

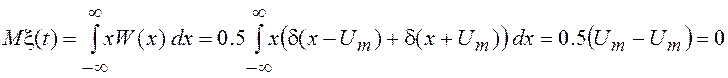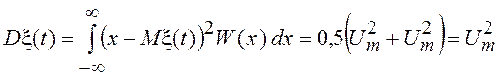Этот результат очевиден, так как квадрат любой реализации есть  для всех t, и результат усреднения с учетом равенства нулю среднего значения дает полученное выше значение .

Найдем теперь корреляционную функцию процесса x(t).

,

поскольку . Произведение  может принимать два значения. Это , если на интервале длиной t произошло четное число перемен знака (М = 0, 2, 4, …) и –, если на этом интервале имело место нечетное число перемен знака  (М = 1, 3, 5, …).  При этом lt – среднее число перемен знака процессом x(t)  на интервале длиной t. Вероятности этих событий равны соответственно 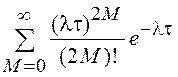 и 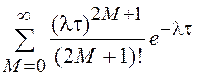. Таким образом,

–=

=.

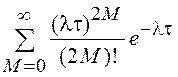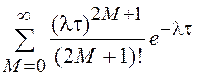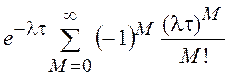Учитывая, равенство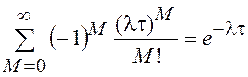 и четность корреляционной функции стационарного процесса, получим окончательно K(t) = . Как и следовало ожидать, K(0) = D x(t) = .

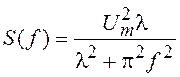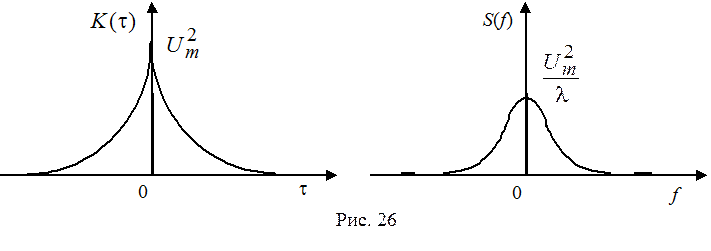
Спектральная плотность, соответствующая полученной K(t), равна . Графики K(t) и S(f) приведены на рис. 26.

Как уже отмечалось, КФ не является исчерпывающей характеристикой СП. СП, реализации которых резко отличаются по форме, могут иметь одинаковые КФ. Так, например, при прохождении «белого» шума с 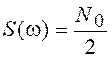 через интегрирующую RC-цепь с коэффициентом передачи 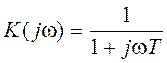, где  - постоянная времени цепи, СПМ на выходе будет иметь вид 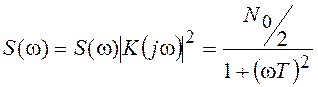. Если положить , то СПМ рассмотренного выше телеграфного сигнала и данного СП совпадут по форме. Следовательно, одинаковую форму будут иметь и КФ этих СП. Выбором значения коэффициента  можно обеспечить полное совпадение КФ и СПМ рассматриваемых процессов. Этот результат понятен. Ведь  и  являются энергетическими характеристиками СП, а форма реализации определяется, в том числе, и фазовым спектром.

Еще раз подчеркнем, что  характеризует скорость изменения СП, которую можно также охарактеризовать средним числом перемен знака СП в единицу времени. Подумать о том, какой вид будут иметь реализации процесса на выходе интегрирующей RC-цепи при подаче на вход «белого» шума, мы предлагаем читателю.

По нашей классификации рассмотренный процесс относится к классу процессов с непрерывным временем и дискретными состояниями. Часто приходится сталкиваться с кусочно-постоянными процессами, у которых изменение состояния происходит в заранее заданные моменты времени, например, в моменты t = kT, где k = 0, ±1, ±2, …, а Т – интервал дискретизации. Такой процесс h(t) можно представить, как результат дискретизации произвольного процесса x(t) с запоминанием отсчетов, взятых в моменты времени t в течение интервала Т. Реализации процессов x(t)  и h(t) приведены на рис.27.

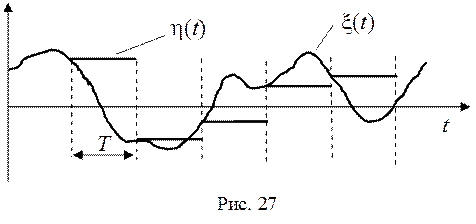
Найдем характеристики процесса h(t), считая x(t) стационарным СП. Очевидно, что математическое ожидание и дисперсия у процессов x(t)  и h(t) одинаковы. Найдем корреляционную функцию процесса h(t), считая, что , и отсчеты процесса x(t) можно считать независимыми СВ. Для простоты рассуждений будем также считать, что Мx(t) = 0. Рассмотрим произведение h(t)h(t – t). Если t > T, то перемножаются независимые СВ, и среднее значение произведения равно произведению средних, а K_h(t) = 0 при |t| > T. Если же t < T, то на интервале Т – t значения h(t) и h(t – t) совпадают, и усреднение дает средний квадрат отсчета, т. е. Dx(t) = s². На интервале же длиной t перемножаются соседние независимые отсчеты, и после усреднения получим произведение средних значений, или 0, в силу условия Мx(t) = 0.

Таким образом, для корреляционной функции процесса h(t) получим:

K_h(t) =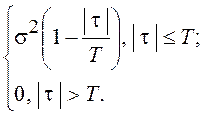

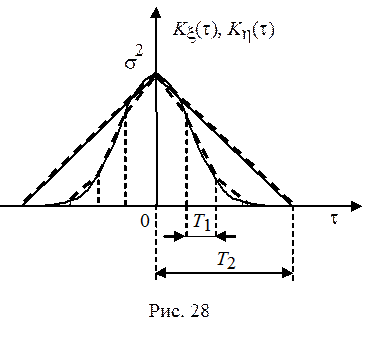
Можно показать, мы предоставляем это читателю, что для общего случая корреляционная функция процесса K_h(t) представляет собой результат линейной аппроксимации K_x(t) с шагом Т, как это показано на рис. 28. На рис. 29. K_x(t) изображена основной линией, а K_h(t) при разных значениях Т –  пунктирной.

Спектральная плотность мощности для случая  имеет вид

.

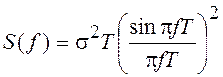Найти спектральную плотность для общего случая мы предлагаем читателю.

Заканчивая первое знакомство с видами случайных процессов, рассмотрим импульсные случайные процессы, которые часто выступают в роли помехи для радиотехнических и телекоммуникационных систем. Остановимся, следуя [8], на нескольких моделях импульсных случайных процессов.