Корреляционные и спектральные характеристики случайных процессов, страница 3

x(t) = Мx(t)  + ,

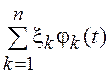где x_k – центрированные (Мx_k = 0), некоррелированные случайные величины с дисперсиями ,  – неслучайные функции. Случайные величины x_k называют коэффициентами, а  – координатными функциями канонического разложения [10].

Рассмотрим вопрос об отыскании координатных функций. Будем считать, что  образуют ортонормальную систему на промежутке . Тогда для коэффициентов  будет справедливо представление

.

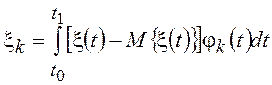Запишем выражение для ковариации коэффициентов , имея в виду, что  = 0

=

=.

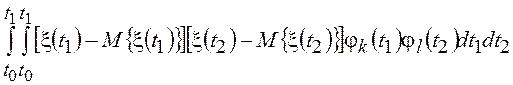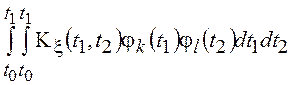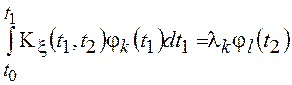Если потребовать выполнения условия , то 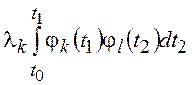 и с учетом ортогональности системы функций  получим требуемый результат 0.

Таким образом, координаты функции являются собственными функциями оператора Фредгольма, ядром которого является корреляционная функция процесса. Нетрудно показать (сделать это читателю предоставляется самостоятельно), что с учетом свойств корреляционной функции этот оператор является симметричным и положительно определенным. Следовательно, его собственные функции действительно образуют ортонормальную систему (см. первую часть пособия, глава 5). Разложение реализаций СП по собственным функциям оператора, порождаемого корреляционной функцией, называется разложением Каруннена-Лоэва.

Рассмотрим более общий случай, когда огибающая r и фаза j являются стационарными СП, т. е. x(t) = r(t) cos(wt – j(t)). Будем также считать, что x(t) – стационарный СП с произвольной ПВ отсчетов W_x(x), которая в силу стационарности x(t)  не зависит от времени. Такие процессы называют квазигармоническими. При сделанных предположениях можно показать [8], что в совпадающие моменты времени огибающая r(t) и фаза j(t) независимы, а отсчеты фазы распределены равномерно в интервале [–p, p] вне зависимости от вида распределения отсчетов процесса x(t), т. е. W(r, j) = W(r)W(j) = W(r). Можно также показать [8], что ПВ огибающей W(r) определяется через характеристическую функцию Q_x(v) процесса x(t) следующим образом:

W(r) = .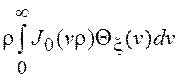

Записанное соотношение является обратным преобразованием Ганкеля, связывающим для данного процесса его ХФ Q_x(v) и ПВ огибающей W(r), в соответствии с которым

.

При этом ПВ отсчетов процесса x(t) должна быть четной функцией W_x(–x) = =W_x(x), а ХФ Q_x(v) – вещественной. Например, если

W_x(x) =,

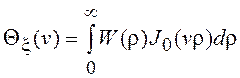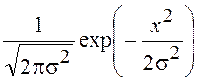т. е., отсчеты x(t) подчинены нормальному закону, то Q_x(v) = 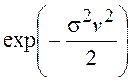 и для ПВ огибающей W(r)  мы получим распределение Рэлея

W(r) =.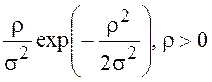

С другим примером квазигармонических процессов можно ознакомиться с помощью [8].

Во многих задачах статистической радиотехники приходится сталкиваться с квазипериодическими стационарными СП вида

x(t) = r(t) F(wt + j(t)),                                        (5.3)

где r(t) и j(t) – стационарные СП, r(t) > 0, | j(t) | < p, F(j) – периодическая функция с периодом 2p, т. е., F(wt + j(t) + 2pk) = F(wt + j(t)), k =0, 1, 2, …. Кроме того, предполагается, что F_max = 1. При F(j) = cosj получаем рассмотренный выше квазигармонический СП. Процесс вида (5.3) описывает, например, случайную последовательность импульсов, форма которых определяется функцией F, а процессы r(t) и j(t) описывают флуктуации амплитуды и параметров импульса (длительность, временное положение) соответственно.

Можно показать [8], что как и для квазигармонического СП, у данного процесса в совпадающие моменты времени отсчеты СП r(t) и j(t) независимы, а “фаза” j распределена равномерно в интервале [–p, p].

Рассмотренные примеры СП относились к четвертому разделу введенной в начале раздела 2 классификации СП (случайные процессы с непрерывными состояниями и непрерывным временем). Приведем примеры СП, относящихся к другим разделам.

Телеграфный сигнал.

Случайный процесс, называемый телеграфным сигналом, может принимать только два значения: +uи –u, а моменты перемены знака – случайны. Пример реализации такого процесса приведен на рис. 25.

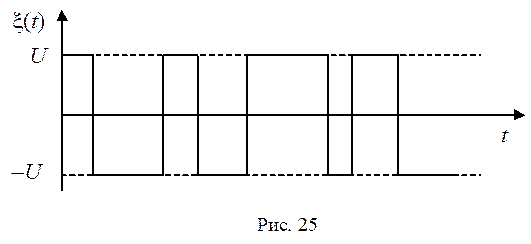
Будем считать, что число перемен знака в единицу времени h подчиняется распределению Пуассона с параметром l: 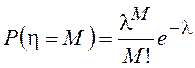. Напомним, что l – среднее значение дискретной СВ h, т. е. среднее число перемен знака процессом x(t) в единицу времени. Процесс x(t) будет стационарным, если l не зависит от времени. ПВ отсчетов данного процесса будет иметь вид:

.