Корреляционные и спектральные характеристики случайных процессов, страница 5

1.  Одиночный импульс со случайным временным положением является случайным процессом вида x(t) = s(t – t₀), где  s(t) – заданная функция, а t₀ – случайная величина с ПВ W(t₀).

2.  Случайная импульсная последовательность x(t) = 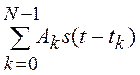, где  s(t), как и ранее,  заданная функция, а А_k и t_k – случайные величины с совместной ПВ W(А₀, А₁, …, A_N–1; t₀, t₁, …, t_N–1). Такой СП является моделью многолучевого канала распространения сигнала в точку приема. Случайные величины  А_k и t_k характеризуют ослабление сигнала и его запаздывание при распространении по k-й траектории (лучу). Для локационных задач данный процесс моделирует отражение зондирующего сигнала от естественных или искусственных отражателей. При этом число отражателей N, как и число лучей, являются дискретными случайными величинами.

Рассмотрим статистические характеристики перечисленных СП. Для одиночного импульса со случайным временным положением среднее значение и корреляционная функция равны соответственно

,

.

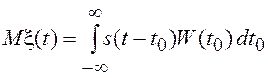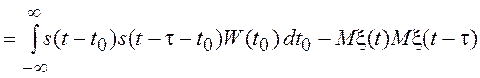Как видно из приведенных выражений, среднее значение является сверткой импульса и ПВ случайной величины t₀, определяющей временное положение импульса, а корреляционная функция  представляет собой свертку ПВ W(t₀) и функции s(t₀) s( t₀ – t).

Если функции s(t₀) и W(t₀) резко различаются по длительности, то одну из них по отношению к другой можно считать “дельта-функцией”. Используя ее фильтрующее свойство, получим следующие приближенные выражения для среднего значения и КФ:

,

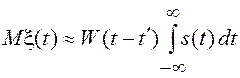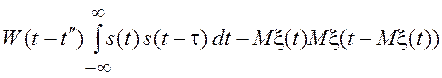
при <<, где  и – длительности функций s(t₀) и W(t₀) соответственно, а t¢ и t² – абсциссы максимумов функций s(t) и s(t) s(t – t).

При << получим:

,

,

где  – абсцисса максимума ПВ W(t₀).

Как видно из приведенных выражений, процесс x(t) в общем случае является нестационарным. Он становится приближенно стационарным в широком смысле, если плотность вероятности W(t₀) = для 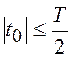 и Т >>. В этом случае

,

.

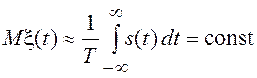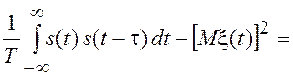
Естественно, этот результат справедлив для .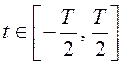

Для случайной импульсной последовательности x(t) = 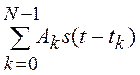 будем считать, что число импульсов N, моменты появления t_k и их амплитудные множители A_k независимы, т. е.

W(N, А₀, А₁, …, A_N–1; t₀, t₁, …, t_N–1) =

= W(N)×W(A₀)× …× W(A_N–1)×W(t₀)×W(t₁)× … ×W(t_N–1),

причем все распределения W(A_k) одинаковы и равны W(A), а распределения моментов появления W(t_k) также одинаковы и равны W(t₀). Тогда, полагая, что моменты появления импульсов подчинены равномерному распределению W(t₀) =  и Т >>, после усреднения по N, A_k и T_k с учетом полученных выше выражений для среднего значения и корреляционной функции, получим:

,

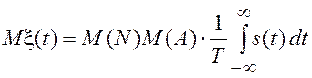=M(N)M(A²)+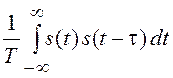

+.

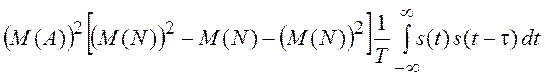Если число импульсов на интервале длиной Т подчиняется распределению Пуассона с параметром l = M(N), а распределение W(A) является симметричным относительно нуля и МА = 0, то  и

=.

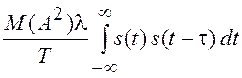Полученной корреляционной функции соответствует СПМ вида

,

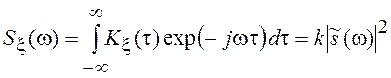где множит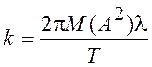ель    характеризует интенсивность данной модели помехи как по уровню (множитель М(А²)), так и по средней относительной частоте появления импульсов (множитель ).

Контрольные вопросы

1. Как связаны между собой КФ и СПМ стационарного СП?

2. Сформулируйте свойства КФ и СПМ стационарного СП.

3. Назовите числовые характеристики КФ и СПМ.

4. Сформулируйте соотношение неопределенности для стационарного СП.

5. Какой процесс называют «белым» шумом, финитным «белым» шумом? Какой вид имеют  и  для названных процессов?

6. Приведите графики (качественно)  и  для СП с гауссовским (колокольным) энергетическим спектром.

7. Случайный процесс , где  - СВ с ПВ 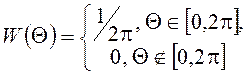 является стационарным. Останется ли он стационарным, если ПВ будет равна 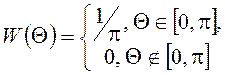? Ответ обосновать.

8. Дайте определение узкополосного процесса.

9. Какой вид в общем случае имеет КФ узкополосного СП?

10. При каких условиях КФ узкополосного СП имеет вид ?

11. Дайте определение комплексного СП.

12. Какой вид имеет  стационарного СП с дискретным энергетическим спектром?

13. Как выглядит каноническое представление СП? Как могут быть найдены координатные функции канонического разложения СП?

14. Каким образом можно сформировать стационарный СП с ?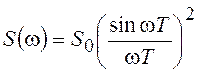

15. Проанализируйте свойства импульсной случайной последовательности 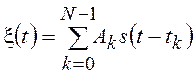, где  - независимые СВ.