Евклидово пространство. Использование неравенства Коши–Буняковского, страница 6

Завершает построение ортогональной системы операция сдвига, при которой функции, соответствующие одному и тому же m сдвигаются так, чтобы они не перекрывались. В результате, после нормировки (умножения полученной функции на ), мы приходим к системе Хаара, рассмотренной выше.

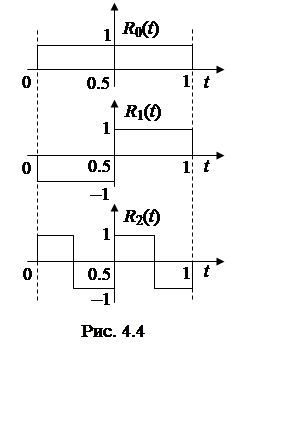
Еще один способ построения ортогональных систем основан на перемножении функций некоторой исходной системы. Рассмотрим в качестве примера систему функций Уолша. За основу при построении системы функций Уолша берутся функции Радемахера , k = 0, 1, 2, … ;
t Î[0, 1], где 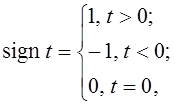 представленные на рис.4.4. Система функций Радемахера не может быть базисной, так как она содержит только нечетные по отношению к середине промежутка [0, 1] функции. Для функций Уолша используют несколько способов упорядочения (нумерации). Для рассматриваемого  способа обычно используют обозначение pal(p, t) и система называется упорядоченной по Пэли. Алгоритм построения системы Уолша–Пэли состоит в следующем. Сперва записывается двоичное представление номера функции ,, после чего  pal(p, t) =. 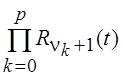Так, например, pal(7, t) =, так как
7 = 2² + + 2¹ + 2⁰.

Наиболее универсальным способом построения ортогональных базисных систем является использование собственных функций линейных операторов. Этот подход мы обсудим после знакомства с элементами теории линейных операторов.

Контрольные вопросы

1.  Сформулируйте аксиомы скалярного произведения.

2.  Запишите неравенство Коши–Буняковского и приведите пример его использования в задачах оптимизации.

3.  Какие вектора называют ортогональными?

4.  Как в евклидовых пространствах норму и метрику согласовывают со скалярным произведением?

5.  Дайте определение гильбертова пространства Н.

6.  Что такое ортогональная система векторов?

7.  Доказать, что, если (, ) = 0 при любом ненулевом векторе , то    = .

8.  Доказать, что любая ортогональная система ненулевых векторов является линейно независимой.

9.  Запишите определитель Грама для системы векторов , k = 1, 2, 3. Какой геометрический смысл он имеет?

10.   Вычислите определитель Грама для системы функций , , , t > 0. Какой вывод можно сделать из полученного результата?

11.   Проверить линейную независимость векторов ₁= (0, –1, 3),
₂= (1, 1, 0), ₃ = (–1, –1, 1) и с помощью процедуры Грама–Шмидта построить ортогональную систему.

12.   Дайте определение взаимного базиса.

13.   Сформулируйте условия полноты и замкнутости ортонормальной системы.

14.   Как вычисляются коэффициенты Фурье функции f(t) для ортонормальной системы .

15.   Сформулируйте экстремальное свойство коэффициентов Фурье  для ортонормальной системы .

16.   Запишите неравенство Бесселя. Дайте ему геометрическую и физическую трактовку.

17.   Дайте определение классических ортогональных многочленов.

18.   Постройте первые три полинома Лагерра (L₀(t), L₁(t), L₂(t)). Интервал ортогональности (0, ¥), весовая функция p(t) = .

19.   Докажите эквивалентность систем функций ,    и   .

20.   Докажите ортогональность системы ,  на отрезке [–p, p]. Превратите ее в ортонормальную систему.

21.   Запишите систему функций Котельникова. Как выбираются параметры F  и  Dt базисной функции?

22.   Как строится система функций Хаара?

23.   Запишите представление R₁(t) и R₂(t) с помощью тригонометрической системы , .

24.   Постройте функцию Уолша  pal(9, t).