При описании ортонормальных
систем в L2 [a, b] ключевыми являются понятия полноты и замкнутости.
Ортонормальная система ![]() полна в L2 [a,
b], если из соотношения
полна в L2 [a,
b], если из соотношения 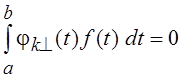 ,
k = 1, 2, … следует, что
,
k = 1, 2, … следует, что
f(t) = 0 почти всюду, т. е., грубо
говоря, допускаются отличия от нуля f(t) в отдельных точках интервала [a,
b]. Сказанное означает, что система полна, если
в L2 [a, b] нет отличной от нуля в указанном выше смысле функции,
ортогональной всем функциям данной системы.
Прежде, чем говорить о
замкнутости, установим одно важное неравенство, называемое неравенством
Бесселя. Пусть ![]() – ортонормальная система в L2
[a, b]. Поставим
в соответствие функции f(t)
из L2 [a, b] линейную комбинацию функций системы
– ортонормальная система в L2
[a, b]. Поставим
в соответствие функции f(t)
из L2 [a, b] линейную комбинацию функций системы 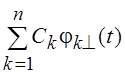 и выясним, при каких значениях
коэффициентов Ck расстояние между f(t) и
и выясним, при каких значениях
коэффициентов Ck расстояние между f(t) и 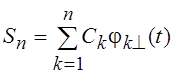 в смысле метрики r2
будет минимально. Таким образом, необходимо найти
в смысле метрики r2
будет минимально. Таким образом, необходимо найти
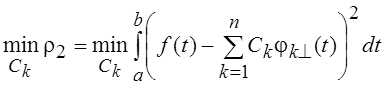 .
.
Записывая необходимое условие экстремума функции п переменных
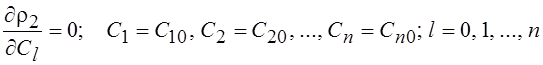 ,
,
получим:
Ck0 = fk = 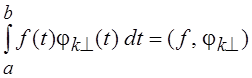 .
.
Эти коэффициенты,
называемые коэффициентами Фурье, определяют для бесконечной ортонормальной
системы ![]() ряд Фурье функции f(t)
ряд Фурье функции f(t) 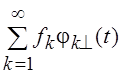 . Часто этот ряд
называют обобщенным рядом Фурье по системе функций
. Часто этот ряд
называют обобщенным рядом Фурье по системе функций ![]() . Таким
образом, коэффициенты Фурье, определяемые для ортонормальной системы
. Таким
образом, коэффициенты Фурье, определяемые для ортонормальной системы ![]() как Ck0 =
как Ck0 = ![]() , обеспечивают среди всех сумм вида Sn =
, обеспечивают среди всех сумм вида Sn = 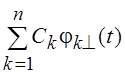 наименьшее
уклонение от f(t)
в смысле метрики r2. Этот факт называют
экстремальным свойством коэффициентов Фурье.
наименьшее
уклонение от f(t)
в смысле метрики r2. Этот факт называют
экстремальным свойством коэффициентов Фурье.
Запишем выражение для квадрата нормы уклонения f(t) от Sn :
![]() =
= 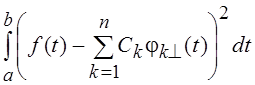 = ||
f ||2 –
= ||
f ||2 – 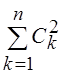 .
.
Так как ![]() для любых f и Sn
(аксиома нормы), то || f ||2 ³
для любых f и Sn
(аксиома нормы), то || f ||2 ³ 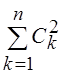 . Это и есть неравенство Бесселя.
. Это и есть неравенство Бесселя.
Дадим геометрическую
трактовку полученному результату. Функция 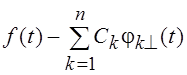 ортогональна
всем линейным комбинациям вида
ортогональна
всем линейным комбинациям вида 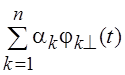 , т.
е. ортогональна линейной оболочке системы
, т.
е. ортогональна линейной оболочке системы ![]() (подпространству,
натянутому на функции
(подпространству,
натянутому на функции ![]() ,
, ![]() , …,
, …, ![]() ) в том и только в том случае, когда Ck = fk =
) в том и только в том случае, когда Ck = fk = ![]() . Таким образом, неравенство Бесселя можно
трактовать как обобщение известной теоремы элементарной геометрии,
утверждающей, что длина перпендикуляра, опущенного из данной точки на прямую
или плоскость, меньше, чем длина любой наклонной, проведенной из той же точки.
. Таким образом, неравенство Бесселя можно
трактовать как обобщение известной теоремы элементарной геометрии,
утверждающей, что длина перпендикуляра, опущенного из данной точки на прямую
или плоскость, меньше, чем длина любой наклонной, проведенной из той же точки.
Можно дать и физическую
интерпретацию неравенства Бесселя. Если рассматривать f(t) Î L2 как падение напряжения на резисторе в 1
Ом, то квадрат нормы || f ||2 = 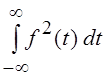 соответствует выделенной энергии Е.
соответствует выделенной энергии Е.
В дальнейшем, когда
элементы L2 будут иметь смысл сигналов, квадрат нормы
сигнала s(t) Î L2
будем также называть энергией сигнала и обозначать как Е, т. е. || s ||2 = 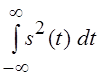 = Е.
= Е.
Энергия соответствующего f(t) ряда Фурье 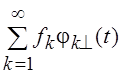 будет равна
будет равна
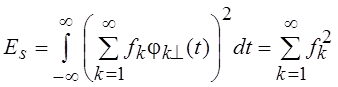 .
.
Таким
образом, в силу ортонормированности системы ![]() величины
величины
![]() имеют смысл энергии k-го
члена обобщенного ряда Фурье (энергии k-й
гармоники) и неравенство Бесселя фиксирует тот факт, что при разложении в
обобщенный ряд Фурье энергия исходной функции (сигнала) не меньше, чем сумма
энергий гармоник.
имеют смысл энергии k-го
члена обобщенного ряда Фурье (энергии k-й
гармоники) и неравенство Бесселя фиксирует тот факт, что при разложении в
обобщенный ряд Фурье энергия исходной функции (сигнала) не меньше, чем сумма
энергий гармоник.
Теперь мы готовы к тому, чтобы дать следующее важное определение.
Ортонормальная система ![]() называется замкнутой в L2
[a, b], если для " f(t) Î L2 [a, b] неравенство Бесселя обращается в равенство Парсеваля,
т. е.
называется замкнутой в L2
[a, b], если для " f(t) Î L2 [a, b] неравенство Бесселя обращается в равенство Парсеваля,
т. е.
|| f ||2 = 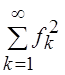 .
(4.4)
.
(4.4)
Обобщением (4.4) является обобщенное равенство Парсеваля, в соответствии с которым для " f(t) и g(t) Î L2 [a, b]
(f, g)
= 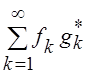 (4.5)
(4.5)
для
комплексного варианта L2 [a,
b] и (f, g) = 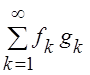 для
вещественного.
для
вещественного.
Доказать (4.5) предлагается читателю.
Для L2 [a, b] понятия замкнутости и полноты эквивалентны.
Среди бесконечномерных евклидовых пространств центральную роль играют так называемые гильбертовы пространства.
Определение.
Гильбертовым пространством называется полное евклидово пространство бесконечного числа измерений*. Обычно оно обозначается буквой Н по фамилии знаменитого немецкого математика Д. Гильберта, который ввел это понятие.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.