Евклидово пространство. Использование неравенства Коши–Буняковского, страница 5

Частные случаи полиномов Якоби
(– 1, 1)	1 – t2	– 2t	1		Полиномы Лежандра
(– 1, 1)	1 – t2	– t			Полиномы Чебышева  I рода
(– 1, 1)	1 – t2	– 3t			Полиномы Чебышева  II рода
(– 1, 1)	1 – t2	– 2(a + 1)t			Ультрасферические полиномы
(0, ¥)	t	a + 1– t, a > – 1			Обобщенные полиномы Лагерра
(–¥, ¥)	1	– 2t			Полиномы Эрмита

Более подробное знакомство с классическими ортогональными полиномами мы отложим до гл.6, посвященной специальным функциям.

Кроме процедуры ортогонализации исходной системы линейно независимых функций существуют и другие способы построения ортогональных систем.

Один из наиболее употребительных состоит в следующем. Выбирается функция, отражающая наиболее характерные особенности множества функций, которые предполагается раскладывать по конструируемой ортогональной системе. Эти особенности могут заключаться в периодичности, финитности преобразования Фурье (ограниченность спектра), непостоянстве поведения (нестационарности) на рассматриваемом промежутке и пр. Параметры этой функции согласовываются с параметрами множества представляемых функций (величина периода, полоса занимаемых частот – ширина спектра). Ортогональная система формируется на базе построенной функции (она называется иногда материнской) с помощью операции масштабирования и (или) сдвига.

Поясним эту процедуру на примерах.

1. Тригонометрическая система.

Тригонометрическая система используется для представления периодических функций, поэтому в качестве материнской функции выбирается функция sin t. Так как эта функция нечетная, то для представления четной составляющей раскладываемой функции необходима функция cos t, которая получается из функции sin t с помощью операции сдвига на p/2. Далее происходит согласование периодов материнской функции и представляемых. Если они имеют период Т, то мы будем использовать функци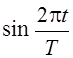и  и 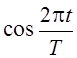. Завершает построение ортогональной системы операция масштабирования  и мы получаем систему 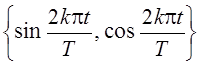, k = 0, 1, 2, ….

2. Базис Котельникова

Как уже отмечалось выше, этот базис используется для представления функций, преобразование Фурье которых 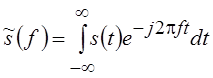 (спектральная функция, спектральная плотность или просто спектр), тождественно равно нулю, если | f | > F.

В качестве материнской используется функция , преобразование Фурье которой равно p при | f | £ 1/2p и нулю при | f | > 1/2p. Для согласования ширины спектра F материнской функции  и представляемых сигналов используется операция масштабирования и мы приходим к функции 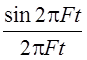, спектр которой тождественно равен нулю при | f | > F.

Для построения ортогональной системы используется операция сдвига k-ой функции системы на время kDt, где Dt = 1/2F, за счет чего получаем 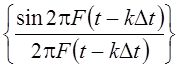, k = 0, ±1, ±2, …. .

Доказательство ортогональности полученной системы и более подробное знакомство с ее свойствами мы отложим до главы, в которой рассматривается преобразование (оператор) Фурье.

3. Система функций Хаара.

Система функций Хаара используется для представления функций, заданных на конечном промежутке [a, b], который с помощью замены 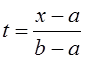 может быть сведен к промежутку [0, 1]. Она оказывается полезной для представления функций, свойства которых (скорость изменения, интенсивность) меняются в пределах [a, b] и соответственно [0, 1]. В качестве материнской выбираем функцию c₂(t), приведенную на рис. 4.1. Функция, равная константе (в данном случае c₁(t) = 1, t Î [0, 1]) присутствует в любой базисной системе и служит для представления постоянной составляющей раскладываемой в ряд функции. 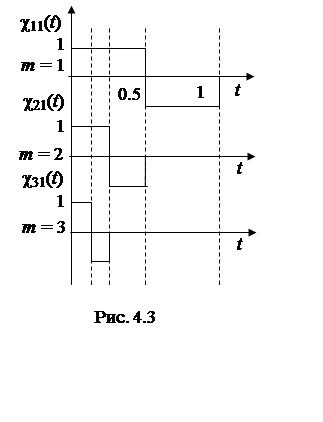Следующая операция – это масштабирование с масштабным коэффициентом 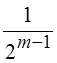, m = 1, 2, …, т. е. переход к функциям , которые изображены на рис. 4.3.