уравнению, в частности каждому дифференциальному уравнению, которому удовлетворяет f1(z).
Стандартный метод
построения аналитического продолжения базируется на использовании ряда Тейлора,
сходящегося в круге ![]() . Для каждой точки z = b
внутри круга значения f(b), f¢(b), … известны и можно записать разложения f(z)
в ряд Тейлора в окрестности точки z = b. Этот новый степенной ряд
сходится внутри круга
. Для каждой точки z = b
внутри круга значения f(b), f¢(b), … известны и можно записать разложения f(z)
в ряд Тейлора в окрестности точки z = b. Этот новый степенной ряд
сходится внутри круга ![]() , часть которого может лежать вне
первого круга. Таким образом, мы получаем аналитическое продолжение f(z)
в часть второго круга, лежащую вне первого. Этот процесс может быть продолжен.
, часть которого может лежать вне
первого круга. Таким образом, мы получаем аналитическое продолжение f(z)
в часть второго круга, лежащую вне первого. Этот процесс может быть продолжен.
6.2. Гамма-функция
Изучение специальных функций во всех руководствах начинается с гамма-функции. Это связано с тем, что знакомство с её свойствами создаёт необходимую базу для изучения других специальных функций.
Рассмотрим хорошо
знакомый из курса математического анализа интеграл 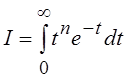 , где n
– целое число. Интегрируя по частям, легко показать, что I = n!, где
, где n
– целое число. Интегрируя по частям, легко показать, что I = n!, где ![]() и
и ![]() . Если теперь рассматривать интеграл
. Если теперь рассматривать интеграл 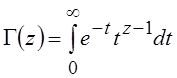 , где
, где ![]() –
комплексное число, причём x > 0, то при произвольных z он не
берётся (не выражается через элементарные функции). Этот интеграл, как функция
параметра z, называется гамма-функцией Эйлера. При
–
комплексное число, причём x > 0, то при произвольных z он не
берётся (не выражается через элементарные функции). Этот интеграл, как функция
параметра z, называется гамма-функцией Эйлера. При ![]() является аналитической функцией и может
быть аналитически продолжена на всю комплексную плоскость.
является аналитической функцией и может
быть аналитически продолжена на всю комплексную плоскость. ![]() аналитична на всей комплексной плоскости
за исключением точек 0, –1, –2, …, –n, в которых она имеет полюса
первого порядка.
аналитична на всей комплексной плоскости
за исключением точек 0, –1, –2, …, –n, в которых она имеет полюса
первого порядка.
Интегрируя ![]() по частям, получим основное функциональное
соотношения
по частям, получим основное функциональное
соотношения ![]() . Если z = n, то последовательное
применение этого соотношения даст нам связь между гамма-функцией и факториалом
. Если z = n, то последовательное
применение этого соотношения даст нам связь между гамма-функцией и факториалом ![]() . Таким образом, гамма-функция обобщает
понятие факториала для произвольных значений аргумента.
. Таким образом, гамма-функция обобщает
понятие факториала для произвольных значений аргумента.
Важную роль при различных преобразованиях и вычислениях выражений, содержащих гамма-функции, играют следующие функциональные соотношения:
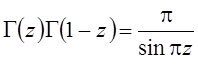 ,
,  .
.
Часто бывает необходимо
знать значение гамма-функции при полуцелом аргументе 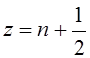 .
Пользуясь первым из записанных соотношений, при
.
Пользуясь первым из записанных соотношений, при 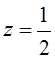 получим:
получим:
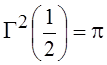 или
или 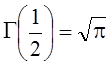 , а на
основе функционального соотношения
, а на
основе функционального соотношения 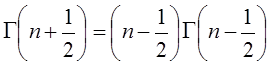 получим окончательно:
получим окончательно:
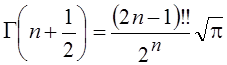 , где
, где
![]() .
.
 Рассмотрим асимптотическое
представление гамма-функции, считая
Рассмотрим асимптотическое
представление гамма-функции, считая
z = x вещественной переменной, причем x >> 1. При решении этой задачи будем пользоваться
методом Лапласа, являющимся частным случаем метода перевала. Рассмотрим
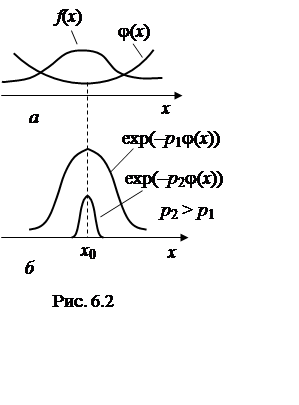
интеграл 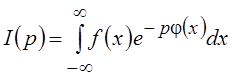 , где p – фиксированное
положительное число, называемое в дальнейшем большим параметром; f(x)
и φ(x) – непрерывные функции. Предположим вначале, что функция φ(x)
имеет один минимум в точке x0
(см. рис.6.2).
, где p – фиксированное
положительное число, называемое в дальнейшем большим параметром; f(x)
и φ(x) – непрерывные функции. Предположим вначале, что функция φ(x)
имеет один минимум в точке x0
(см. рис.6.2).
При больших значениях p существенным является поведение функции φ(x) в малой окрестности точки минимума x0. Разлагая функцию φ(x) в ряд Тейлора в окрестности точки x = x0 и удерживая первые три члена, получим:
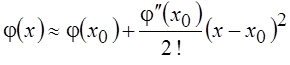 .
.
Заметим, что в точке x0 функция φ(x) имеет минимум, поэтому ![]() , а
, а ![]() .
Считая далее, что функция f(x) мало меняется в области, в которой
отлична от нуля функция
.
Считая далее, что функция f(x) мало меняется в области, в которой
отлична от нуля функция ![]() (чем больше p,
тем уже эта область и справедливее это предположение), и полагая
(чем больше p,
тем уже эта область и справедливее это предположение), и полагая ![]() , получим:
, получим:
 .
.
После замены переменной ![]() и вычисления интеграла получим
окончательно:
и вычисления интеграла получим
окончательно:
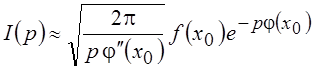 .
(6.6)
.
(6.6)
Полученная формула без труда обобщается и на случай, когда функция φ(x) имеет несколько минимумов в области интегрирования. В этом случае
 , (6.7)
, (6.7)
где х1, х2, …, хп – точки минимума функции φ(x). Вывод формул (6.6), (6.7) базировался на предположении, что функция f(x) не меняется в малой окрестности точки x0. Более точный результат можно получить, если функцию f(x) разложить в ряд Тейлора в окрестности точки x0, т. е.
 .
.
Меняя местами операции
суммирования и интегрирования и выполняя замену переменной 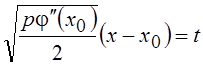 , получим:
, получим:
 ,
(6.8)
,
(6.8)
или с учётом того, что интеграл в (6.8) при нечётных k равен нулю,
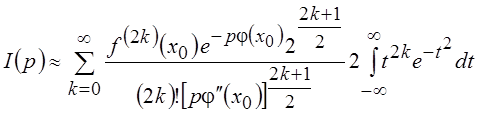 . (6.9)
. (6.9)
Интеграл, входящий в (6.9), равен
 , 6.10)
, 6.10)
в чем можно убедиться, дифференцируя k раз по a левую и правую части равенства 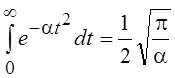 и полагая затем a = 1.
и полагая затем a = 1.
Подставляя (6.10) в (6.9) и учитывая,
что ![]() , где (2k)!! – произведение последовательных чётных чисел от 2 до
2k включительно, получим окончательно:
, где (2k)!! – произведение последовательных чётных чисел от 2 до
2k включительно, получим окончательно:
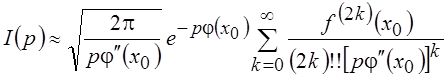 .
(6.11)
.
(6.11)
Естественно, что формула
(6.11) может быть обобщена и на случай, когда функция φ(x) имеет
несколько минимумов. При интегрировании по конечному или полубесконечному
интервалу и использовании полученных формул возникают дополнительные ошибки,
связанные с тем, что максимум функции ![]() может
располагаться достаточно близко к краям интервала интегрирования [a, b] или к левому краю интервала
может
располагаться достаточно близко к краям интервала интегрирования [a, b] или к левому краю интервала ![]() . При этом замена интеграла
. При этом замена интеграла 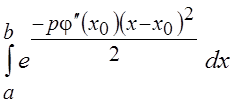 на
на 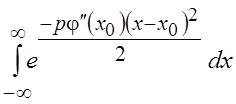 справедлива
лишь в том случае, когда подынтегральная функция равна нулю вне интервала [a, b]. Очевидно, величина ошибки,
связанной с такой заменой, зависит от положения точки x0 внутри [a, b] и большого параметра p. Чем больше p, тем
меньше ошибка за счёт “краевого эффекта”.
справедлива
лишь в том случае, когда подынтегральная функция равна нулю вне интервала [a, b]. Очевидно, величина ошибки,
связанной с такой заменой, зависит от положения точки x0 внутри [a, b] и большого параметра p. Чем больше p, тем
меньше ошибка за счёт “краевого эффекта”.
Для применения метода Лапласа представим Γ(x) в следующем виде:
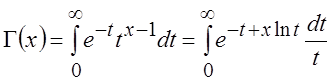 и
сделаем замену переменной
и
сделаем замену переменной ![]() , после чего вынесем
множитель
, после чего вынесем
множитель ![]() за знак интеграла.
за знак интеграла.
После этих преобразований получим:
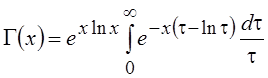 .
.
В соответствии с методом Лапласа x
– большой параметр, ![]() ,
, 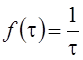 ,
поэтому первое приближение для Γ(x) будет иметь вид:
,
поэтому первое приближение для Γ(x) будет иметь вид:
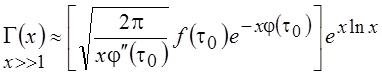 ,
,
где τ0 – точка минимума функции φ(τ), определяемая из уравнения
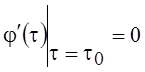 ,
,  ,
, ![]() .
.
Вторая производная функции φ(τ)
равна ![]() , а её значение в точке τ0 равно 1, поэтому окончательно получим:
, а её значение в точке τ0 равно 1, поэтому окончательно получим:
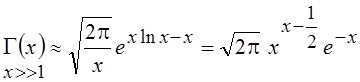 .
.
Погрешность этого представления не
превышает величины 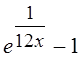 . Асимптотическая формула для
факториала имеет вид
. Асимптотическая формула для
факториала имеет вид
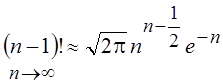 .
.
Ошибка не превышает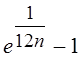 .
.
Через гамма-функцию может быть выражен обширный класс определённых
интегралов. Для приложений особый интерес представляет интеграл вида  , x > 0,
y > 0, называемый Эйлеровым интегралом
первого рода или бета-функцией.
, x > 0,
y > 0, называемый Эйлеровым интегралом
первого рода или бета-функцией.
Можно показать, что
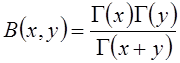 .
.
Гамма- и бета-функции широко используются в теории вероятностей, задавая весьма универсальные модели случайных величин, имеющих гамма и бета распределения. Функции распределения этих величин описываются с помощью неполных гамма- и бета-функций (g(x, y) и Bz(x, y) соответственно), определяемых следующим образом:
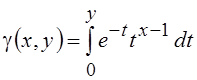 ;
; 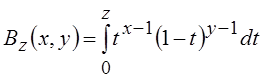 .
.
Соответствующие функции распределения имеют вид
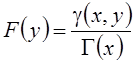 ;
;  .
.
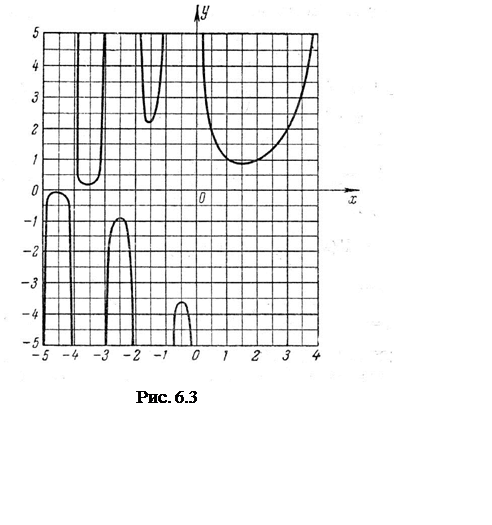
В заключение параграфа
приведём график гамма-функций (рис. 6.3). Как уже отмечалось выше, Γ(x)имеет в точках z = 0,
–1, –2, –3,… полюса, поэтому гамма-функция Γ(x) имеет в этих
точках вертикальные асимптоты с чередованием знаков в полюсах. При положительных
целочисленных значениях аргументов x = n гамма-функция совпадает со значением
факториала (п – 1)!.
6.3. Интеграл вероятностей и функции с ним связанные
Интегралом вероятностей называют интеграл вида
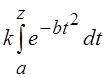 , (6.12)
, (6.12)
где a и z в общем случае комплексные величины, z – переменная, k и b – кон-
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.