Практикум "Математические модели в экономике": семинары и домашние задания

Teacher: Татьяна Владимировна Сумская

Subject: Математические модели в экономике: seminars and home works

Часть I. Экономическая статистика.. 1

1.0. Введение: основные понятия.. 1

1.1. Целевые установки экономического развития.. 8

1.1.1. Многоцелевая (векторная) оптимизация.. 8

1.1.2. Многокритериальная оптимизация.. 9

1.1.3. Взаимные задачи.. 11

1.2. Модели частичного равновесия (принцип рациональности в поведении отдельных хозяйственных субъектов). 14

1.2.1. Моделирование сферы потребления.. 14

1.2.1.1. Целевая функция потребления. 14

1.2.1.2. Классическая модель потребителя. 15

1.2.1.3. Предложение труда в модели поведения потребителя. 29

1.2.1.4. Межвременной выбор. 30

1.2.1.5. Элементы теории общего равновесия. 31

Часть I. Экономическая статистика

1.0. Введение: основные понятия

1)  Валовой выпуск (ВВ), конечное потребление (КП), валовой внутренний продукт (ВВП), валовой национальный продукт (ВНП).

2)  Бюджетный дефицит, общий бюджет, государственный долг (внутренний и внешний).

3)  Темп роста, темп прироста.

4)  Материалоемкость, трудоемкость, производительность труда (ПТ), фондоёмкость (ФЁ), фондоотдача (ФО), нормативные отчисления от прибыли предприятия.

5)  Налоги (прямые, косвенные).

6)  Стабилизационная политика.

7)  Дисконтирование.

8)  Постановка задачи математического программирования, двойственной задачи, теорема Куна-Таккера, дополняющей нежесткости и т.д.…

9)  Обратная матрица, собственные числа, собственные вектора.

10) Решения дифференциальных уравнений.

Найти (x₁,…, x_n) при которых: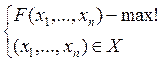

Теорема Вейерштрасса:

Если допустимое множество X не пусто и компактно (замкнуто и ограничено), а целевая функция f(x), определенная на данном множестве является непрерывно дифференцируемой, тогда эта функция достигает глобального максимума во внутренней или граничной точке данного множества.

Пусть X – не пусто, компактно и выпукло, f(x) – непрерывно дифференцируема и вогнута на X, тогда локальный максимум является глобальным, а множество точек на которых достигается этот максимум выпукло.

Множество S выпукло, если

Классическая задача математического программирования:

F(x) – max!

g(x)=b, g – непрерывно дифференцируемая функция.

x=(x₁,…, x_n)

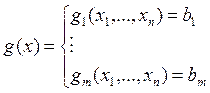
Если n>m, то можно построить функцию Лагранжа:

L(x,y)=F(x)+y(b-g(x))

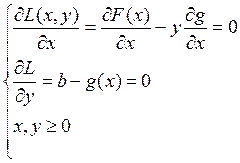
Не линейная задача математического программирования:

F(x) – max!

g(x)≤b

x≥0

Условия Куна-Таккера (необходимое условие максимума):

x* - максимум тогда и только тогда, когда существует y* такой, что (x*,y*) удовлетворяет следующему:

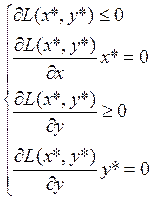
y – множитель Лагранжа – показывает как изменяется целевая функция при изменении прпавой части ограничений на малую величину.

Линейная задача математического программирования:

Если допустимое множество не пусто, и целевая функция имеет ограничение (снизу и сверху), тогда множество решений не пусто.

Условия дополняющей нежесткости:

Если ; Если

Если ; Если

Темп роста и темп прироста:

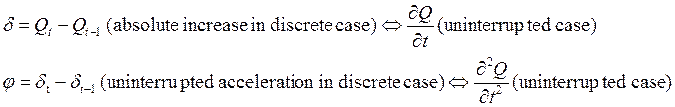
Темп прироста:

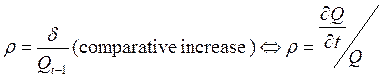
Темп роста:

1)  Цепной:

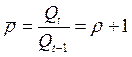
2)  Базисный:

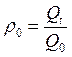
Произведение цепных темпов роста равен базисному темпу роста.

Показатели предприятия:

Фондоотдача: 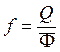(общий выпуск за год к среднегодовой стоимости основных фондов)

Фондоёмкость: 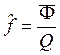. Для государства в целом: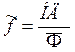

Фондовооруженность: 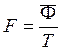(T – среднегодовая численность занятых)

Трудоемкость: 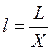(используемый труд к произведенному продукту)

Производительность труда:

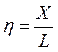
Материалоемкость: = 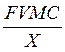 (Фонд Возмещения Материальных Затрат)

Линейная алгебра:

A=(a_ij) – квадратная матрица порядка n с действительными элементами

A-λE – характеристическая матрица

|A-λE| - характеристическое уравнение для A

Ax=λx

(A-λE)x=0, λ – собственное число, x – собственный вектор.

Норма A – максимальная сумма по столбцам.

Теорема Фабьенуса-Перрона:

Предположим, что матрица A имеет положительное собственное число (корень Фабьенуса-Перрона), превосходящее по модулю все прочие собственные числа этой матрицы и соответствующий ему строго положительный вектор .При этом собственный вектора соответствующие, отличным от собственным числам обязательно имеют компоненты разных знаков.

Корень Фабьенуса-Перрона () заключается между максимальными и минимальными суммами по столбцам.

Макроэкономика:

Гос. долг (ГД) – накопленная сумма дефицитов гос. бюджета.

Обслуживание долга – выплата основной суммы долга и процентов по нему.

Первичный дефицит – дефицит бюджете без учета расходов по обслуживанию долга.

Задача 1.0.1

Предприятие выпускает продукцию тремя способами. Задано соотношение между текущими и капитальными затратами. Известен спрос на продукцию и ограничение на капитальные вложения. Выбрать наиболее эффективный способ.