Задача 49
а) 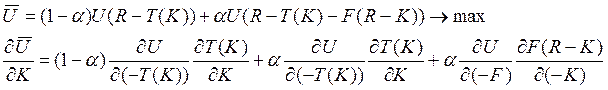
Ну и от сюда, можно сделать некоторые умозаключенияJ по различным соотношениям между полезностью и переменными в задаче.
б) Если μ – доля скрываемого дохода, и ее можно изменять, как это отразится на целевой функции? Очевидно, это отразится на его доходе, который он показываетJ, одновременно, перепишем и условие:
K-(1-μ)R<0, тогда с вероятностью α факт сокрытия обнаружат, и индивид платит налог T(K)+F(R-K) и штраф. Чтоб не обнаружили – K=(1-μ)R. Больше – делать экономически не эффективно, но мы и рассматриваем, рационального агента.
Поэтому задача перепишется:
![]()
в) В общем случае ,такую задаче решить мне не под силу J Пусть, например, для значительного облегчения расчетов функция предпочтений задана квазилинейной функцией – U=a1x1+a2lnx2
Оптимальный спрос:
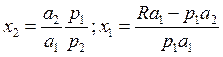
Поскольку 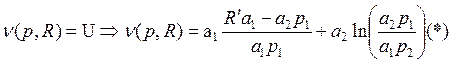
Где 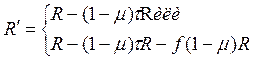
Требуется узнать, какую долю своего дохода индивиду оптимальнее показывать J
Для этого надо продифференцировать (*) по μ. Но от μ зависит только R`, поэтому:
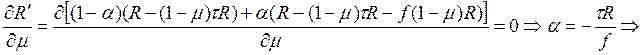 достижение максимально располагаемого
дохода не зависит от выбора μ.
достижение максимально располагаемого
дохода не зависит от выбора μ.
г) Определим величину скрываемого дохода исходя из функции полезности (при скрываемом доходе):
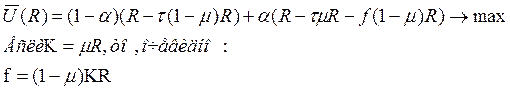
Подставляя последнее
выражение в ![]() и дифференцируя по μ, получим, что
и дифференцируя по μ, получим, что 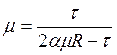 . Видно ,что при росте дохода, доля
скрываемого дохода сокращается. ЧТД.
. Видно ,что при росте дохода, доля
скрываемого дохода сокращается. ЧТД.
1.2.1.3. Предложение труда в модели поведения потребителя
Задача 52
U(x,h)=x(h+2)
X – блага, l – работа. Q=16, R=20, px=25, ph=10.
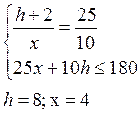
а) 25x=(10(16-h)+20)(1-t)
б)25x=10(16-h)(1-t)+20
в) 25x(1+t)=10(16-h)+20
г)25x=10(16-h1-h2)+20
Ответы:
а) h=8; x=4(1-t)
б) h=7+1/(1-t); x=2/5*(9+(1/(1-t))(1-t))
в) h=8; x=4/(1+t)
г) h=8; x=50/13
Эффект Лаффера:
а) T=100t (нет)
б) T=(80t-90t2)/(1-t) (есть)
в) T=100t/(1+t) (нет)
Задача 53
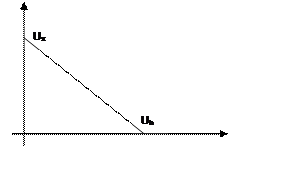
![]()
Очевидно, решение – угловое:
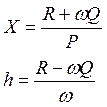
Задача 54
U(x,h)=x2
l+h=7*16=112
w=4
l=60, h=52, p=100
а)Бюджетное ограничение: 100x≤4l-(4l-150)t, l=112-h
100x+4(1-t)h≤448-298t
h=(448-298t)/(12(1-t))
б) если l≤60 à h≥52 à (448-298t)/(12(1-t))≥52àt0.54
в) T=(298-4h)t=(298-(448-298t)/(3(1-t)))t=…=(446t-596t2)/3(1-t)
Берем производную по T, приравниваем к нулю, два корня, один – больше единицы – не подходит, другой – 0.49≈0.5
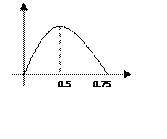 Эффект Лаффера есть.
Эффект Лаффера есть.
1.2.1.4. Межвременной выбор
Задача 56
(1+r)p1x1+p2x2/(1+r)=R1+R2/(1+r) |*(1+r)
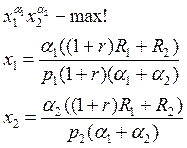
Задача 58
U(X)=a1lnx1+a2lnx2
S=R1-p1x1
p2x2=R2+(1+r)S
p2x2=R2+(1+r)(R1-p1x1)
(1+r)p1x1+p2x2≤(1+r)R1+R2
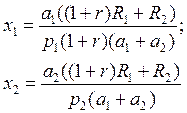
Задача 59
Следует рассмотреть два случая. Первый – не учитывать его ожидания à он не сохраняет, помимо S, некоторую долю, в расчете на то, что станет безработным и сохраняет. Пусть эта доля – β.
Рассмотрим второй вариант.
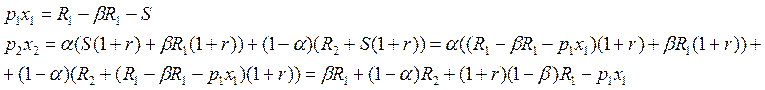
Если он станет безработным с вероятностью 1, то будет жить за счет сделанных сбережений.
При первом варианте, то есть когда он уверен, что не станет безработным и бичего не сберегает, однако если на самом деле он стал безработным ,есть ему нечего будет. L
1.2.1.5. Элементы теории общего равновесия
Задача 62
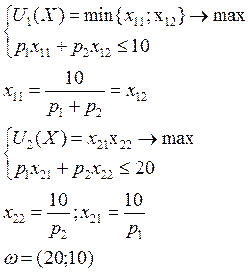
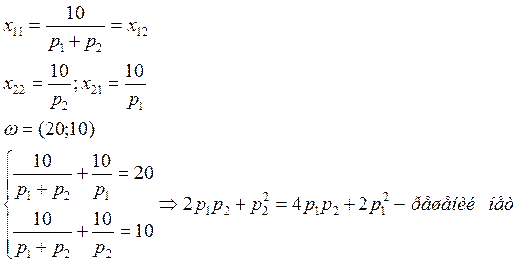
Задача 63
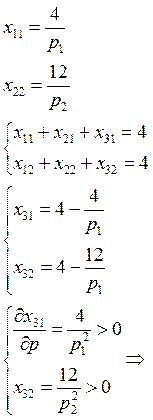 товар Гиффена. ЧТД.
товар Гиффена. ЧТД.
Задача 64
Так как функции полезности линейны, то оптимальное решение – га осях, в зависимости от наклона бюджетного ограничения:
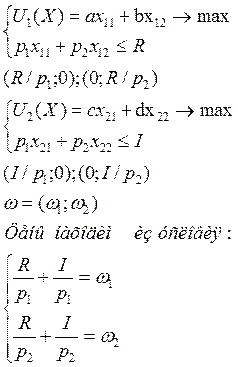
Задача 65
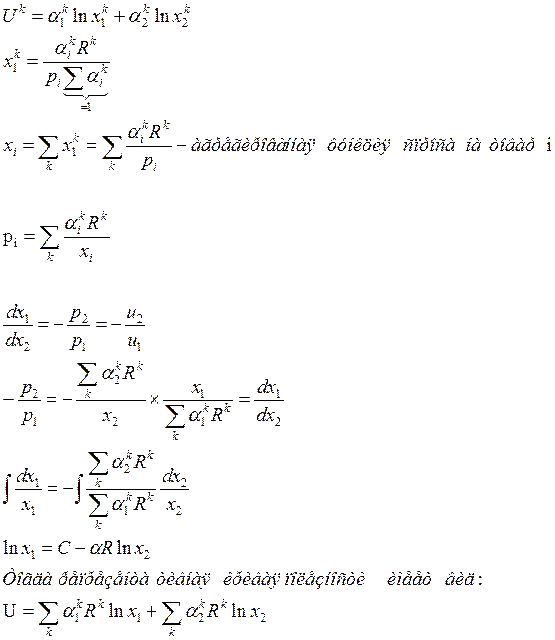
Задача 66
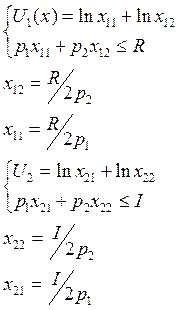
Задача 67
Избыточный спрос в равновесии равен нулю, откуда:
p2=3, p1=4; x1=E1+1, x2=2
4x1+3x2+3x3=10
Избыточный спрос для x3:
x3=13-4x1-3x2
x4=-p1+p2+2
x3=p1+2p2-7
Производная x3 по первой цене =1 и по второй цене = 2, тоже больше нуля, поэтому товары взаимодополняемые.
Задача 68
а) 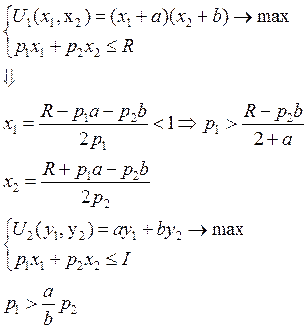 б)
б) 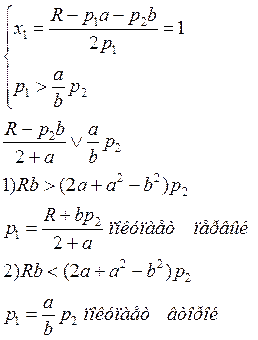
[1] СОП – совокупный общественный продукт, ФВ – фонд возмещения, ФН – фонд накопления, ФП – фонд потребления, ОПФ – основные производственные фонды,
[2] НЗП – незавершенное производство, НЗС – незавершенное строительство.
[3] Интегральный фонд потребления – это сумма фондов потребления за определенный период времени.
[4] (1+) - инвестиционный лаг; - амортизация; NE=EX-m(1-a)X [IM]
[5] (*) – «лишнее», поэтому можно продавать для увеличения выпуска.
[6] Здесь и далее – задачи из сборника задач Бересневой, Комаровой. То, что xi не отрицательны во всех задачах подразумевается автоматически, если не оговорено обратное.
[7] Цветом выделены домашние задания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.